
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=90°﹣∠BDO.
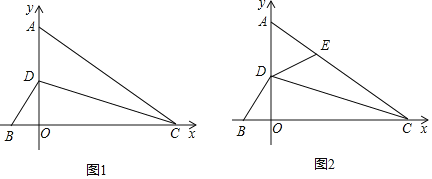
(1)求证:AC=BC;
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长.
【答案】(1)见解析;(2)8
【解析】
(1)由题意∠CAO=90°﹣∠BDO,可知∠CAO=∠CBD,CD平分∠ACB与y轴交于D点,所以可由AAS定理证明△ACD≌△BCD,由全等三角形的性质可得AC=BC;
(2)过D作DN⊥AC于N点,可证明Rt△BDO≌Rt△EDN、△DOC≌△DNC,因此,BO=EN、OC=NC,所以,BC+EC=BO+OC+NC﹣NE=2OC,即可得BC+EC的长.
(1)证明:∵∠CAO=90°﹣∠BDO,
∴∠CAO=∠CBD.
在△ACD和△BCD中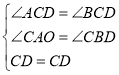 ,
,
∴△ACD≌△BCD(AAS).
∴AC=BC;
(2)由(1)知∠CAD=∠DEA=∠DBO,
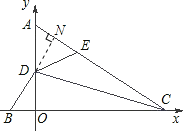
∴BD=AD=DE,过D作DN⊥AC于N点,如图所示:
∵∠ACD=∠BCD,
∴DO=DN,
在Rt△BDO和Rt△EDN中![]() ,
,
∴Rt△BDO≌Rt△EDN(HL),
∴BO=EN.
在△DOC和△DNC中,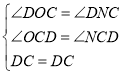
∴△DOC≌△DNC(AAS),
∴OC=NC;
∴BC+EC=BO+OC+NC﹣NE=2OC=8.


科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题.
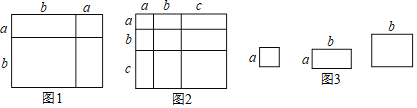
(1)写出图2中所表示的数学等式 ;
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2;
(4)利用(1)中得到的结论,直接写出代数式![]() 展开之后的结果:
展开之后的结果:![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形ABDE和ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
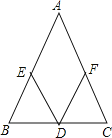
【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.
(1)你添加的条件是
(2)在(1)的条件下,不再添加辅助线和字母,证明DE=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用三角尺可按如图所示的方法画角平分线:已知∠AOB,把一个三角尺的一个顶点放在点O处,一条直角边放在OB上,过直角顶点C作OB的垂线DC;再用同样的方法作OA的垂线EF, EF与DC交于点P.作射线OP,则OP即为∠AOB的平分线.这样作图的依据是构造两个三角形全等,由作法可知,△EPO≌△CPO的依据是( ).
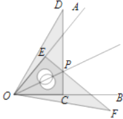
A.SASB.HLC.ASAD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图(1)所示).图(2)由弦图变化得到,它是由八个全等的直角三角形拼接而成的记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若EF=4,则S1+S2+S3的值是( )
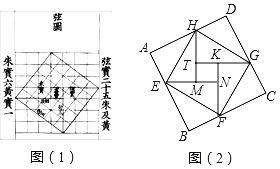
A.32B.38C.48D.80
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com