
【题目】如图,点A、点B是双曲线![]() 图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.

【答案】-8
【解析】
由四边形AEDC的面积等于△BEO的面积,OD=DC可知S△ABE=S△OED,所以S△OAB=S△OAC,所以AB=AC,可知E为△OCB的重心,进而可知BE=2DE,所以S△OED=![]() S△BEO=2,可知S△OBC=12,设B(a,b)、A(m,n),则a=2m,b=
S△BEO=2,可知S△OBC=12,设B(a,b)、A(m,n),则a=2m,b=![]() ,根据A、B两点坐标可求出直线AB的解析式,即可求出C点的坐标,即OA的长,利用△OBC的面积求出mn =k的值即可.
,根据A、B两点坐标可求出直线AB的解析式,即可求出C点的坐标,即OA的长,利用△OBC的面积求出mn =k的值即可.
∵由四边形AEDC的面积等于△BEO的面积,OD=DC,
∴S△ABE=S△OED,
∴S△OAB=S△OAC,
∴AB=AC,即点E为△OCB的重心,
∴BE=2DE,
∴S△OED=![]() S△BEO=2,
S△BEO=2,
∴S△OBC=12,
∵AB=AC,
∴a=2m,
∵b=![]() ,
,![]() ,
,
∴b=![]() ,
,
∴直线AB的解析式为:![]() ,
,
∴C点坐标为:(0,![]() ),
),
∴S△OBC=![]()
![]() ∣
∣![]() ∣
∣![]() ∣2m∣=12
∣2m∣=12
解得:∣mn∣=8,
∵m<0,n>0,
∴mn=-8,
∵A点在双曲线![]() 图象上,
图象上,
∴mn=k,
∴k=-8.
故答案为:-8


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,真命题的是( )
A.两边和一角对应相等,两三角形全等
B.两腰对应相等的两等腰三角形全等
C.两角和一边对应相等,两三角形全等
D.两锐角对应相等的两直角三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
若a是正整数,则长度为![]() 的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是
的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是![]() .
.

(1)在图1中以A为一个端点,画出一条长为![]() 的线段AC;
的线段AC;
(2)![]() (空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为
(空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为![]() ;
;
(3)利用材料所给的方法,直接写出三边长分别为![]() 、
、![]() 、
、![]() 的三角形的面积:__________.
的三角形的面积:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如果两个三角形两边和其中一边所对的角相等,则两个三角形全等,这是一个假命题,请画图举例说明;
(2)如图,在△ABC和△DEF中,AB=ED,BC=DF,∠BAC=∠DEF=120°,求证:△ABC≌△EDF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 是关于
是关于![]() 的二次函数.求:
的二次函数.求:
![]() 满足条件的
满足条件的![]() 的值;
的值;
![]() 为何值时,抛物线有最低点?求出这个最低点,这时当
为何值时,抛物线有最低点?求出这个最低点,这时当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 为何值时,函数有最大值?最大值是多少?这时当
为何值时,函数有最大值?最大值是多少?这时当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而减小?
的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题.
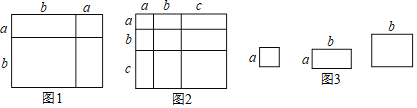
(1)写出图2中所表示的数学等式 ;
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2;
(4)利用(1)中得到的结论,直接写出代数式![]() 展开之后的结果:
展开之后的结果:![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.

(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,有一个五角星ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=![]() 吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
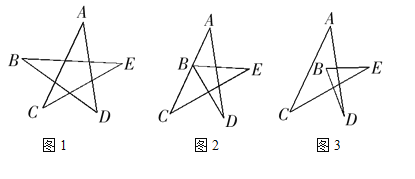
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com