
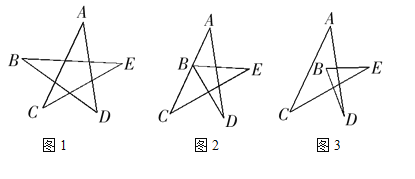
【题目】如图1,有一个五角星ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=![]() 吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
【答案】成立,理由见解析
【解析】
由三角形内角和外角的关系可把五个角的度数归到一个三角形中,再由三角形内角和定理即可求出答案.
解:如图(一),∵∠1是△BDF的外角,
∴∠B+∠D=∠1,同理∠A+∠C=∠2,
由三角形内角和定理可知∠1+∠2+∠E=180°,即,∠B+∠D+∠A+∠C+∠E=180°;如图(二)∵∠1是△ABD的外角,
∴∠A+∠D=∠1,同理∠E+∠EBD=∠2,
由三角形内角和定理可知∠1+∠2+∠C=180°,即,∠EBD+∠D+∠A+∠C+∠E=180°;
如图(三),∵∠2是△ACN的外角,
∴∠C+∠A=∠2,同理∠D+∠B=∠1,
由三角形内角和定理可知∠1+∠2+∠E=180°,即,∠B+∠D+∠A+∠C+∠E=180°,故结论都成立.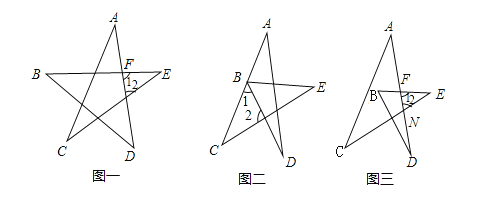


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
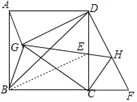
【题目】如图,在边长为2![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是_____.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、点B是双曲线![]() 图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.
图象上的两点(A在B的右侧).延长AB交y轴正半轴于C,OC的中点为D.连结AO,BO,交点为E.若△BEO的面积为4,四边形AEDC的面积等于△BEO的面积,则k的值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
设从甲养殖场调运鸡蛋x斤,总运费为W元
(1)试写出W与x的函数关系式.
(2)怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1.

(1)判断△BEC的形状,并说明理由?
(2)判断四边形EFPH是什么特殊四边形?并证明你的判断;
(3)求四边形EFPH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标的原点是等边三角形的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com