
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

【答案】(1)证明见解析;(2)∠BED=45°.
【解析】试题分析:(1)由等边三角形的性质知∠BAC=60°,AB=AC,由旋转的性质知∠DAE=60°,AE=AD,从而得∠EAB=∠DAC,再证△EAB≌△DAC可得答案;
(2)由∠DAE=60°,AE=AD知△EAD为等边三角形,即∠AED=60°,继而由∠AEB=∠ADC=105°可得.
试题解析:(1)∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵线段AD绕点A顺时针旋转60°,得到线段AE,
∴∠DAE=60°,AE=AD.
∴∠BAD+∠EAB=∠BAD+∠DAC.
∴∠EAB=∠DAC.
在△EAB和△DAC中,
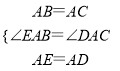 ,
,
∴△EAB≌△DAC.
∴∠AEB=∠ADC.
(2)如图,


∵∠DAE=60°,AE=AD,
∴△EAD为等边三角形.
∴∠AED=60°,
又∵∠AEB=∠ADC=105°.
∴∠BED=45°.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是__________,从点燃到燃尽所用的时间分别是________;
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)燃烧多长时间,甲、乙两根蜡烛的高度相同?(不考虑都燃尽时的情况)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=1,将△ABC绕点C顺时针旋转60°至△A′B′C,点A的对应点A′恰好落在AB上,求BB′的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直线交于点E,过点D作DF∥BE交BC所在直线于点F.

(1)如图1,AB<AD,
①求证:四边形BEDF是菱形;
②若AB=4,AD=8,求四边形BEDF的面积;
(2)如图2,若AB=8,AD=4,请按要求画出图形,并直接写出四边形BEDF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列语句,设适当的未知数,列出二元一次方程:
![]() 甲数比乙数的
甲数比乙数的![]() 倍少
倍少![]() ;
;
![]() 甲数的
甲数的![]() 倍与乙数的
倍与乙数的![]() 倍的和是
倍的和是![]() ;
;
![]() 甲数的
甲数的![]() 与乙数的
与乙数的![]() 的差是
的差是![]() ;
;
![]() 甲数与乙数的和的
甲数与乙数的和的![]() 倍比乙数与甲数差的
倍比乙数与甲数差的![]() 多
多![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF= ![]() ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 ![]() 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,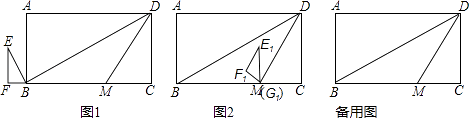
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com