
【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF= ![]() ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 ![]() 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,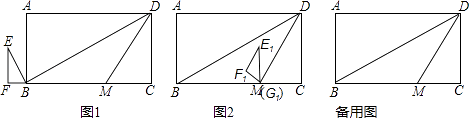
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
【答案】
(1)3
(2)
解:在Rt△DCM中,∵∠C=90°,CD=6,∠CDM=30°,
∴CM=2 ![]() ,DM=4
,DM=4 ![]() ,
,
∴BM=4 ![]() .
.
①如图2中,当0<t≤4时,重叠部分是四边形NF1GH,

S=S ![]() ﹣S
﹣S ![]() =
= ![]() ×3×
×3× ![]() ﹣
﹣ ![]() (2
(2 ![]() ﹣
﹣ ![]() t)(2﹣
t)(2﹣ ![]() t)=﹣
t)=﹣ ![]() t2+2
t2+2 ![]() t﹣
t﹣ ![]()
![]() ,
,
②如图3中,当4<t≤7时,重叠部分是四边形GHNF1,

S=S ![]() ﹣S
﹣S ![]() =
= ![]() ﹣
﹣ ![]() [2
[2 ![]() ﹣
﹣ ![]() (8
(8 ![]() ﹣
﹣ ![]() t)][2﹣
t)][2﹣ ![]() (8﹣t)]=﹣
(8﹣t)]=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() ,
,
③如图4中,当7<t≤8时,重叠部分是△GHN,

S= ![]()
![]() (8
(8 ![]() ﹣
﹣ ![]() t)
t) ![]() (8
(8 ![]() ﹣
﹣ ![]() t)=
t)= ![]() t2﹣6
t2﹣6 ![]() t+24
t+24 ![]() ,
,
综上所述,S= 
(3)
解:存在.
理由:①如图5中,当∠DQP=90°时,

∵∠QCM=∠CQF2=∠QF2M=90°,
∴四边形MCQF2是矩形,
∴CQ=MF2= ![]() ,∠F2MC=90°
,∠F2MC=90°
∴α=90°,DQ=CD﹣CQ=6= ![]() .
.
②如图6中,当∠DPQ=90°时,点P与点F2重合,点E、Q、C重合,此时α=120°,DQ=CD=6.

综上所述,当α=90°,DQ=6﹣ ![]() 或α=120°,DQ=6时,△DPQ为直角三角形
或α=120°,DQ=6时,△DPQ为直角三角形
【解析】解:(1)如图1中,连接AC交BD于点O,作OH⊥BC于点H.
∵四边形ABCD是矩形,
∴AB=CD=6,BO=OD,
∴BH=HC,
∴OH= ![]() CD=3,
CD=3,
在Rt△DBC中,∵CD=6,∠DBC=30°,
∴BC=6 ![]() ,BD=12,BH=HC=3
,BD=12,BH=HC=3 ![]()
∵在△EFG中,∠F=90°,GF= ![]() ,∠E=30°,
,∠E=30°,
∴EF=3,EB=2 ![]() ,
,
∴当△E1F1G1的顶点E1恰好在BD上时,点E平移到点O处.
此时t= ![]() =3,
=3,
∴t=3时,△E1F1G1的顶点E1恰好在BD上,
所以答案是3.
【考点精析】关于本题考查的翻折变换(折叠问题),需要了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月﹣5月明明一家减少了驾车出行,他们将2月﹣5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图: 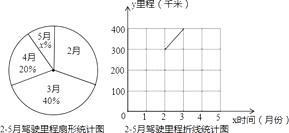
(1)扇形统计图中x= , 并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应的大括号内.
3![]() ,-
,-![]() ,
,![]() ,0.5,2π,3.14159265,-
,0.5,2π,3.14159265,-![]() ,1.103030030003…(相
,1.103030030003…(相
邻两个3之间依次多1个0).
(1) 有理数集合:{ };
(2) 无理数集合:{ };
(3) 实数集合:{ };
(4) 负实数集合:{ }.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,△A1B1C1和△A2B2C2的顶点都在方格纸的格点上. 
(1)求△A1B1C1和△A2B2C2的面积比.
(2)点A1、D、E、F、G、H是△A1B1C1边上的6个格点,请在这6个格点中选取3个点作为三角形的顶点,使构成的三角形与△A2B2C2相似(要求写出2个符合条件的三角形,并分别在图1和图2中将相应三角形涂黑,不必说明理由).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com