
【题目】把下列各数填入相应的大括号内.
3![]() ,-
,-![]() ,
,![]() ,0.5,2π,3.14159265,-
,0.5,2π,3.14159265,-![]() ,1.103030030003…(相
,1.103030030003…(相
邻两个3之间依次多1个0).
(1) 有理数集合:{ };
(2) 无理数集合:{ };
(3) 实数集合:{ };
(4) 负实数集合:{ }.
科目:初中数学 来源: 题型:
【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证: 
(1)EH=FH;
(2)∠CAB=2∠CDH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF= ![]() ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 ![]() 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,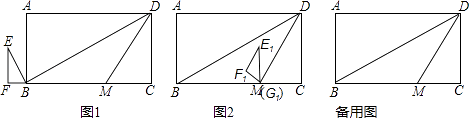
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12cm,BC=8cm.点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向移动.点E、G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2) 
(1)当t=1秒时,S的值是多少?
(2)写出S和t之间的函数解析式,并指出自变量t的取值范围;
(3)若点F在矩形的边BC上移动,当t为何值时,以点E、B、F为顶点的三角形与以点F、C、G为顶点的三角形相似?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题: 
(1)设这个苗圃园垂直于墙的一边的长为x米,则平行于墙的一边长为;(用含x的代数式表示)
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0)的图象与函数y=x﹣ ![]() 的图象如图所示,则下列结论:①ab>0;②c>﹣
的图象如图所示,则下列结论:①ab>0;②c>﹣ ![]() ;③a+b+c<﹣
;③a+b+c<﹣ ![]() ;④方程ax2+(b﹣1)x+c+
;④方程ax2+(b﹣1)x+c+ ![]() =0有两个不相等的实数根.其中正确的有( )
=0有两个不相等的实数根.其中正确的有( ) 
A.4 个
B.3 个
C.2 个
D.1 个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com