
【题目】第一象限内两点![]() ,
,![]() ,点P在x轴上,若
,点P在x轴上,若![]() 最小,则Р点坐标为________.
最小,则Р点坐标为________.
【答案】![]()
【解析】
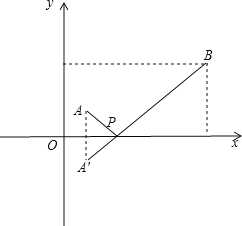
先画出图形,由两点之间线段最短可知,作出A点对称点,连接A'B交x轴于一点,此点就是点P,即PA+PB=A'B,此时PA+PB最小,求得直线A'B的解析式为y=x﹣2,当y=0时,x=2,即可得到结论.
作点A关于x轴的对称点A',则A'坐标为(1,﹣1),
连接A'B交x轴于一点,此点就是点P,此时PA+PB最小,
作BE⊥y于一点E,延长A'A交BE于一点M.
∵PB=PA',∴PA+PB=BA'.
∵A、B两点的坐标分别为(1,1)和(5,3),A'坐标为(1,﹣1),
设直线A'B的解析式为:y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线A'B的解析式为:y=x﹣2,
当y=0时,x=2,∴P(2,0).
故答案为:(2,0).


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E在AD边上,过点E作AB的平行线,交BC于点F,将矩形ABFE绕着点E逆时针旋转,使点F的对应点落在边CD上,点B的对应点N落在边BC上.
(1)求证:BF=NF;
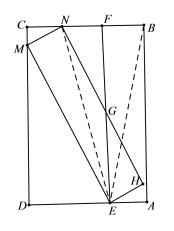
(2)已知AB=2,AE=1,求EG的长;
(3)已知∠MEF=30°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题.
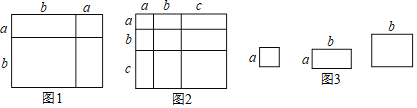
(1)写出图2中所表示的数学等式 ;
(2)根据整式乘法的运算法则,通过计算验证上述等式;
(3)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,求a2+b2+c2;
(4)利用(1)中得到的结论,直接写出代数式![]() 展开之后的结果:
展开之后的结果:![]() =
=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.

(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
查看答案和解析>>
科目:初中数学 来源: 题型:
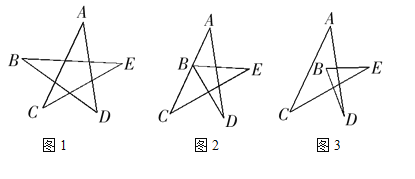
【题目】如图1,有一个五角星ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=![]() 吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
吗? 如图2、图3,如果点B向右移到AC上,或AC的另一侧时,上述结论仍然成立吗?请分别说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传统节日“端午节”的早晨,小文妈妈为小文准备了四个粽子作早点:一个枣馅粽,一个肉馅粽,两个花生馅粽,四个粽子除内部馅料不同外,其它一切均相同.
(1)小文吃前两个粽子刚好都是花生馅粽的概率为 ;
(2)若妈妈在早点中给小文再增加一个花生馅的粽子,则小文吃前两个粽子都是花生馅粽的可能性是否会增大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
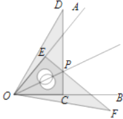
【题目】用三角尺可按如图所示的方法画角平分线:已知∠AOB,把一个三角尺的一个顶点放在点O处,一条直角边放在OB上,过直角顶点C作OB的垂线DC;再用同样的方法作OA的垂线EF, EF与DC交于点P.作射线OP,则OP即为∠AOB的平分线.这样作图的依据是构造两个三角形全等,由作法可知,△EPO≌△CPO的依据是( ).
A.SASB.HLC.ASAD.SSS
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com