
【题目】如图,矩形ABCD中,点E在AD边上,过点E作AB的平行线,交BC于点F,将矩形ABFE绕着点E逆时针旋转,使点F的对应点落在边CD上,点B的对应点N落在边BC上.
(1)求证:BF=NF;
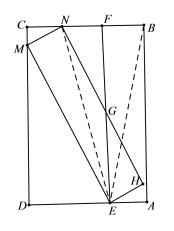
(2)已知AB=2,AE=1,求EG的长;
(3)已知∠MEF=30°,求![]() 的值.
的值.
【答案】(1)详见解析;(2)EG=![]() ;(3)
;(3)![]() .
.
【解析】
(1)连结BE,EN,根据旋转的性质可知BE=EN,由∠EFB=90°,根据等腰三角形底边的高是底边中线即可证明BF=NF.(2)根据旋转的性质可证明△NGF≌△HGE,进而证明FG=GH,根据勾股定理求出GE的长即可.(3)根据EF//CD可知∠MEF=DME=30°,由旋转性质可知∠EMN=90°,进而可知∠CNM=30°,设DE=x,则ME=2x,MD=![]() x,进而可求出CM的长,即可求出MN的长,根据BC=DE+MN即可求出BC的长,进而求出答案.
x,进而可求出CM的长,即可求出MN的长,根据BC=DE+MN即可求出BC的长,进而求出答案.
(1)连结BE,EN,如图,
∵四边形ABCD是矩形,
∴∠BFE=90°,
由旋转得BE=EN,
∴BF=NF;
(2)∵四边形ABCD是矩形,
∴BF=AE,EF=AB,
由旋转得EH=EA,
∵BF=NF,
∴EH=NF,
∵∠BFE=∠GHE=90°,∠NGF=∠HGE,
∴△NGF≌△HGE,
∴FG=GH,
设GE=x,则GF=GH=2﹣x,
由勾股定理得x2﹣(2﹣x)2=1,
解得x=![]() ,
,
∴EG=![]() ;
;
(3)∵EF∥DC,
∴∠DME=∠MEF=30°,
设DE=x,
∵∠D=90°,
∴ME=DC=AB=2x,DM=![]() x,
x,
∴MC=(2﹣![]() )x,
)x,
∵∠NME=90°,∠DME=30°,
∴∠NMC=60°,
∴∠MNC=30°,
∴MN=2MC=2(2﹣![]() )x,
)x,
∴BC=AD=DM+MN=2(2﹣![]() )x+x=(5﹣2
)x+x=(5﹣2![]() )x,
)x,
∴![]() =
=![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() ,现把一块直径为
,现把一块直径为![]() 的量角器(圆心为
的量角器(圆心为![]() )放置在图形上,使其
)放置在图形上,使其![]() 线
线![]() 与
与![]() 重合;若将量角器
重合;若将量角器![]() 线上的端点
线上的端点![]() 固定在点
固定在点![]() 上,再把量角器绕点
上,再把量角器绕点![]() 顺时针方向旋转
顺时针方向旋转![]() ,此时量角器的半圆弧与
,此时量角器的半圆弧与![]() 相交于点
相交于点![]() ,设点
,设点![]() 处量角器的读数为
处量角器的读数为![]() .
.

![]() 用含
用含![]() 的代数式表示
的代数式表示![]() 的大小;
的大小;
![]() 当
当![]() 等于多少时,线段
等于多少时,线段![]() 与
与![]() 平行?
平行?
![]() 在量角器的旋转过程中,过点
在量角器的旋转过程中,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .设
.设![]() ,
,![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
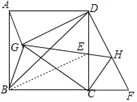
【题目】如图,在边长为2![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是_____.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示:

(1)根据图示填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 |
|
|
高中部 | 85 |
|
|
(2)结合两队成绩的平均数中中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手的成绩较为稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com