Question

【题目】已知：平面直角坐标系中，点A（a，b）的坐标满足|a﹣b|+b2﹣8b+16＝0．

（1）如图1，求证：OA是第一象限的角平分线；

（2）如图2，过A作OA的垂线，交x轴正半轴于点B，点M、N分别从O、A两点同时出发，在线段OA上以相同的速度相向运动（不包括点O和点A），过A作AE⊥BM交x轴于点E，连BM、NE，猜想∠ONE与∠NEA之间有何确定的数量关系，并证明你的猜想；

（3）如图3，F是y轴正半轴上一个动点，连接FA，过点A作AE⊥AF交x轴正半轴于点E，连接EF，过点F点作∠OFE的角平分线交OA于点H，过点H作HK⊥x轴于点K，求2HK+EF的值．

Answer 1

【答案】（1）证明见解析 （2）答案见解析 （3）8

【解析】

（1）过点A分别作x轴，y轴的垂线，垂足分别为M、N，则AN＝AM,

根据非负数的性质求出a、b的值即可得结论；

（2）如图2，过A作AH平分∠OAB，交BM于点H，则△AOE≌△BAH，可得AH＝OE，由已知条件可知ON=AM，∠MOE＝∠MAH，可得△ONE≌△AMH，∠ABH＝∠OAE，设BM与NE交于K，则∠MKN＝180°﹣2∠ONE＝90°﹣∠NEA，即2∠ONE﹣∠NEA＝90°；

（3）如图3，过H作HM⊥OF，HN⊥EF于M、N，可证△FMH≌△FNH，则FM＝FN，同理：NE＝EK，先得出OE+OF﹣EF＝2HK，再由△APF≌△AQE得PF＝EQ，即可得OE+OF＝2OP＝8，等量代换即可得2HK+EF的值．

解：（1）∵|a﹣b|+b2﹣8b+16＝0

∴|a﹣b|+（b﹣4）2＝0

∵|a﹣b|≥0，（b﹣4）2≥0

∴|a﹣b|＝0，（b﹣4）2＝0

∴a＝b＝4

过点A分别作x轴，y轴的垂线，垂足分别为M、N，则AN＝AM

∴OA平分∠MON

即OA是第一象限的角平分线

（2）过A作AH平分∠OAB，交BM于点H

∴∠OAH＝∠HAB＝45°

∵BM⊥AE

∴∠ABH＝∠OAE

在△AOE与△BAH中

，

∴△AOE≌△BAH（ASA）

∴AH＝OE

在△ONE和△AMH中

，

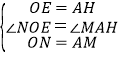∴△ONE≌△AMH（SAS）

∴∠AMH＝∠ONE

设BM与NE交于K

∴∠MKN＝180°﹣2∠ONE＝90°﹣∠NEA

∴2∠ONE﹣∠NEA＝90°

（3）过H作HM⊥OF，HN⊥EF于M、N

可证：△FMH≌△FNH（SAS）

∴FM＝FN

同理：NE＝EK

∴OE+OF﹣EF＝2HK

过A作AP⊥y轴于P，AQ⊥x轴于Q

可证：△APF≌△AQE（SAS）

∴PF＝EQ

∴OE+OF＝2OP＝8

∴2HK+EF＝OE+OF＝8