
【题目】如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.

(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(3,1),在此坐标系下,B点的坐标为 ;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为 ;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c的图象过O、B、C三点,D为此抛物线的顶点。试求出抛物线解析式及D点的坐标。
【答案】(1)建立坐标系详见解析,(1,2);(2)线段BC详见解析,(2,0); (3)![]() ,D(1,
,D(1,![]() ).
).
【解析】
(1)建立坐标系如图,满足A点坐标为(-3,-1),在此坐标系下,得到B点坐标;
(2)在(1)图中作出线段BC,求出C点坐标;
(3)将O、B、C三点坐标代入二次函数解析式中,解方程得到二次函数的解析式,将所求的二次函数的解析式化简,求出顶点D的坐标.
(1)建立坐标系如图,
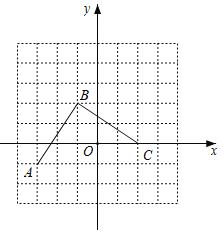
∴B点的坐标为(1,2);
故答案为:(1,2);
(2)线段BC如图所示,
C点的坐标为(2,0);
故答案为:(2,0);
(3)∵C点的坐标为(2,0),O(0,0),B(1,2)
∴所求二次函数解析式为![]()
∴![]()
∴D(1,![]() )
)


科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+![]() x+2与直线y=
x+2与直线y=![]() x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
x+2相交于点C和D,点P是抛物线在第一象限内的点,它的横坐标为m,过点P作PE⊥x轴,交CD于点F.
(1)求点C和D的坐标;
(2)求抛物线与x轴的交点坐标;
(3)如果以P、C、O、F为顶点的四边形是平行四边形,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
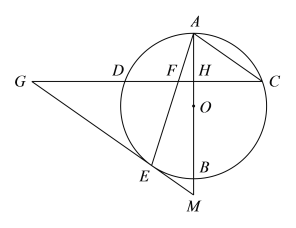
(1)求证:EG是⊙O的切线;
(2)延长AB交GE的延长线于点M,若AH=2,![]() ,求OM的长.
,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
若a是正整数,则长度为![]() 的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是
的线段是有可能表示正方形网格中两个格点之间的距离(设小正方形的长度为单位1).如图1所示,A、B两点之间的距离就是![]() .
.

(1)在图1中以A为一个端点,画出一条长为![]() 的线段AC;
的线段AC;
(2)![]() (空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为
(空格处填正整数,两组数要求不一样),并根据你填的数字,在图2中画出两种对应的线段,其长度均为![]() ;
;
(3)利用材料所给的方法,直接写出三边长分别为![]() 、
、![]() 、
、![]() 的三角形的面积:__________.
的三角形的面积:__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如果两个三角形两边和其中一边所对的角相等,则两个三角形全等,这是一个假命题,请画图举例说明;
(2)如图,在△ABC和△DEF中,AB=ED,BC=DF,∠BAC=∠DEF=120°,求证:△ABC≌△EDF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 是关于
是关于![]() 的二次函数.求:
的二次函数.求:
![]() 满足条件的
满足条件的![]() 的值;
的值;
![]() 为何值时,抛物线有最低点?求出这个最低点,这时当
为何值时,抛物线有最低点?求出这个最低点,这时当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 为何值时,函数有最大值?最大值是多少?这时当
为何值时,函数有最大值?最大值是多少?这时当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而减小?
的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.

(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.请根据以上信息回答:
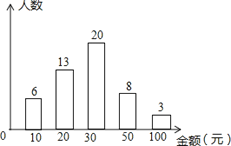
(1)该班同学所抢红包金额的众数是______,
中位数是______;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com