
【题目】如图,在圆![]() 中有折线
中有折线![]() ,
,![]() ,
,![]() ,
,![]() ,则弦
,则弦![]() 的长为_____.
的长为_____.

【答案】10
【解析】
作OD⊥AB垂足为D,利用垂径定理得AB= 2BD ,作OE//AB交BC于E,构造等边△COE ,过E点作EF⊥AB,垂足为F,得Rt△BEF,而∠B= 60° ,可得BF= ![]() BE ,再根据BD= BF+ DF,求BD.
BE ,再根据BD= BF+ DF,求BD.
如图,作OD⊥AB垂足为D,作OE//AB交BC于E,过E点作EF⊥AB,垂足为F,
∵OE//AB,∴△COE为等边三角形,∴OE= CE= OC= 4,∵OD⊥AB,EF⊥AB,∴ DF= OE= 4,BE= BC- CE= 2,在Rt△BEF中,∵∠B= 60°,∴BF=![]() BE=1,∴BD=BF+DF=1+4=5,由垂径定理,得AB=2BD=10,故答案为10.
BE=1,∴BD=BF+DF=1+4=5,由垂径定理,得AB=2BD=10,故答案为10.


科目:初中数学 来源: 题型:
【题目】(1)![]() 的绝对值是___________,相反数是___________.
的绝对值是___________,相反数是___________.
(2)计算下列各式:
①![]()
②![]()
(3)无理数![]() 的整数部分是( )
的整数部分是( )
A.1 B.2 C.3 D.4
(4)对于实数a,如果将不大于a的最大整数记为![]() ,则
,则![]() =_____________
=_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (
(![]() )的对称轴为直线
)的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为
轴的一个交点坐标为![]() ,其部分图象如图所示,下列结论:①
,其部分图象如图所示,下列结论:①![]() ;②方程
;②方程![]() 的两个根是
的两个根是![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当
;⑤当![]() 时,
时,![]() 随
随![]() 增大而增大.其中结论正确的个数是( )
增大而增大.其中结论正确的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.

(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(3,1),在此坐标系下,B点的坐标为 ;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为 ;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c的图象过O、B、C三点,D为此抛物线的顶点。试求出抛物线解析式及D点的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
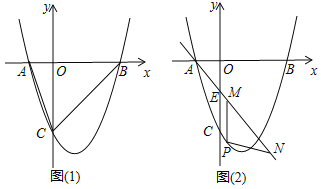
【题目】如图(1),抛物线![]() 与x轴交于A(1,0)、B(t,0)(t >0)两点,与y轴交于点C(0,3),若抛物线的对称轴为直线x=1,
与x轴交于A(1,0)、B(t,0)(t >0)两点,与y轴交于点C(0,3),若抛物线的对称轴为直线x=1,
(1)求抛物线的函数解析式;
(2 若点D是抛物线BC段上的动点,且点D到直线BC的距离为![]() ,求点D的坐标
,求点D的坐标
(3)如图(2),若直线y=mx+n经过点A,交y轴于点E(0,1),点P是直线AE下方抛物线上一点,过点P作x轴的垂线交直线AE于点M,点N在线段AM延长线上,且PM=PN,是否存在点P,使△PMN的周长有最大值?若存在,求出点P的坐标及△PMN的周长的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A市有近20年的马拉松比赛历史,过去全程马拉松名额一直相对较少。而近几年,这一现状大大改变,很多想参加全程马拉松(简称全马)的跑者报不上名。所以该城市近两年也大幅增加“全马”的名额。2017年,参加“全马”的人数比“半马”的人少,但是2018年,2019年参加“全马”的人数呈上升趋势,且每年比前一年均增加25%(即2018年比2017年增加25%,2019年比2018年增加25%),2019年,有12500名“全马”参赛者。
(1)求2017年、2018年“全马”参赛人数;
(2)据赞助食物的某商家反映:2017年与2018年该商家分别给参加“全马”和“半马”的参赛者提供了不同价格的食物,每个“全马”参赛者获得的食物价值高于“半马”参赛者,2017年,商家提供食物共用去22万元;这两年商家是按同一个标准分别给“全马”和“半马”参赛者提供食物(人太多,标准不可轻易提高),即使这样,2018年,虽然参加马拉松比赛的总人数与2017年一样多,但是由于“全马”参赛者人数刚好与“半马”参赛者人数调换了,赞助商比2017年多提供了p万元的食物;商家发现这p万元的食物刚好可以供400名“全马”参赛者和400名“半马”参赛者享用。求p的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一元二次方程![]() 满足
满足![]() ,那么我们称这个方程为“凤凰”方程.已知
,那么我们称这个方程为“凤凰”方程.已知![]() 是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
是“凤凰”方程,且有两个相等的实数根,则下列结论正确的是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com