练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）的绝对值是___________，相反数是___________．

    （2）计算下列各式：

    ①

    ②

    （3）无理数的整数部分是（ ）

    A．1 B．2 C．3 D．4

    （4）对于实数a，如果将不大于a的最大整数记为，则=_____________

    【答案】(1)，；(2)①-4；②；(3)B；(4) ．

    【解析】

    （1）根据实数绝对值和相反数的求法问题可解；（2）根据平方根、立方根以及实数的相关性质对各式进行化简后进行加减运算即可；（3）估算出的范围问题可解；（4）先求出的范围，再求出的范围问题可解.

    解：(1)∵

    ∴的绝对值是

    的相反数是-（）=；

    故答案为：，.

    (2)①

    ②

    (3) ∵<<

    ∴ 2<<3

    无理数的整数部分是2

    故应选B

    (4)，

    ∴，

    ∴，故答案为：．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校举办了一次趣味数学竞赛，满分100分，学生得分均为整数，达到成绩60分及以上为合格，达到90分及以上为优秀，这次竞赛中，甲乙两组学生成绩如下，甲组：30,60,60，60,60,60,70,90,90,100 ；乙组：50,60,60,60,70,70,70,70,80,90.

    （1）以上成绩统计分析表中a=______分，b=______分，c=_______分；

    组别

    平均数

    中位数

    方差

    合格率

    优秀率

    甲组

    68分

    a

    376

    30%

    乙组

    b

    c

    90%

    （2）小亮同学说：这次竞赛我得了70分，在我们小组中属于中游略偏上，观察上面表格判断，小亮可能是甲乙哪个组的学生？并说明理由

    （3）计算乙组的方差和优秀率，如果你是该校数学竞赛的教练员，现在需要你选一组同学代表学校参加复赛，你会选择哪一组？并说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为1，AC，BD是对角线，将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：

    ①四边形AEGF是菱形；②△HED的面积是1﹣；③∠AFG=112.5°；④BC+FG=．其中正确的结论是（　　）

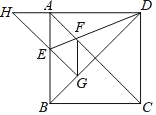
    A. ①②③ B. ①②④ C. ①③④ D. ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连接AC，过上一点E作EG∥AC交CD的延长线于点G，连接AE交CD于点F，且EG=FG．

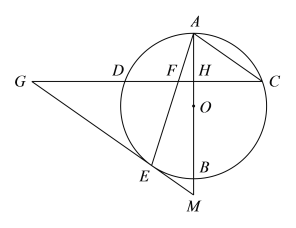
    （1）求证：EG是⊙O的切线；

    （2）延长AB交GE的延长线于点M，若AH=2，，求OM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A的坐标为（﹣2，0），等边△AOC经过平移或轴对称或旋转都可以得到△OBD．

    （1）△AOC沿x轴向右平移得到△OBD，则平移的距离是　 　个单位长度；△AOC与△BOD关于直线对称，则对称轴是　 　；△AOC绕原点O顺时针旋转得到△DOB，则旋转角度可以是　 　度．

    （2）连接AD，交OC于点E，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】材料阅读：

    若a是正整数，则长度为的线段是有可能表示正方形网格中两个格点之间的距离（设小正方形的长度为单位1）．如图1所示，A、B两点之间的距离就是．

    （1）在图1中以A为一个端点，画出一条长为的线段AC；

    （2）（空格处填正整数，两组数要求不一样），并根据你填的数字，在图2中画出两种对应的线段，其长度均为；

    （3）利用材料所给的方法，直接写出三边长分别为、、的三角形的面积：__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在圆中有折线，，，，则弦的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数是关于的二次函数．求：

    满足条件的的值；

    为何值时，抛物线有最低点？求出这个最低点，这时当为何值时，随的增大而增大？

    为何值时，函数有最大值？最大值是多少？这时当为何值时，随的增大而减小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等边△ABC中，点D为射线BA上一点，作DE=DC，交直线BC于点E,∠ABC的平分线BF交CD于点F，过点A作AH⊥CD于H，当EDC=30，CF=，则DH=______．

    查看答案和解析>>

    同步练习册答案