
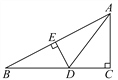
【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30![]() ,CF=
,CF=![]() ,则DH=______.
,则DH=______.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,一次函数y1=x+m与反比例函数y2=![]() 的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
的图象相交于A(2,1),B(n,﹣2)两点,与x轴交于点C.
(1)求反比例函数解析式和点B坐标;
(2)当x的取值范围是 时,有y1>y2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】镇江某特产专卖店销售某种特产,其进价为每千克40元,若按每千克60元出售,平均每天可售出100千克,经过市场调查发现,单价每降低3元,平均每天的销售量可增加30千克,专卖店销售这种特产若想要平均每天获利2240元,且销售尽可能大,则每千克特产应定价为多少元?
(1)解:方法1:设每千克特产应降价x元,由题意,得方程为:_____;
方法2:设每千克特产降低后定价为x元,由题意,得方程为:_____.
(2)请你选择一种方法,写出完整的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,DE垂直平分AB,交BC于点D,连接AD,若AC=8,DC:AD=3:5.求:
(1)CD的长;
(2)DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边三角形ABC的边长为3,过AB边上一点P作PE![]() AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为_________________.
AC于点E,Q为BC延长线上一点,取PA=CQ,连接PQ,交AC于M,则EM的长为_________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,抛物线y=-x2+bx+c的顶点M在直线AB上,且抛物线与直线AB的另一个交点为N.
(1)如图,当点M与点A重合时,求抛物线的解析式;
(2)在(1)的条件下,求点N的坐标和线段MN的长;
(3)抛物线y=-x2+bx+c在直线AB上平移,是否存在点M,使得△OMN与△AOB相似?若存在,直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com