
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。

【答案】(1)证明见解析 (2)![]() (3)
(3)![]()
【解析】
(1) 连接OB,根据OB=OC得出∠1=∠2,再根据CB平分∠ACE,得出∠2=∠3,再利用平行线的性质求解即可;(2) 连接DF,根据同弧所对圆周角相等得出∠CDF=∠CBF,再利用直径所对的圆周角为90°,得出∠DFC=90°,由OB//CE,得出△AOB∽△ACE,利用相似三角形的性质,列出方程求解即可;(3) 先证出△ACB∽△BCF,再利用相似三角形的性质得出![]() =
=![]() ,进而求出结果.
,进而求出结果.
(1)证明:如图1,连接OB,
∵OB=OC,∴∠1=∠2,
∵CB平分∠ACE,∴∠2=∠3,
∴∠1=∠3,∴OB∥CE,
∴∠ABO=∠AEC=90°,即OB丄AE,
∴AE是⊙0的切线;
(2)如图2,连接DF,
∵∠CDF和∠CBF是同弧所对圆周角,
∴∠CDF=∠CBF,
∵CD是⊙O的直径,∴∠DFC=90°,
∴DF//AE,∴∠A=∠CDF,∴∠A=∠CBF,
∵cos∠CBF=![]() ,∴cosA=
,∴cosA=![]() ,
,
在Rt△ACE中AE=8,∴AC=10,CE=6,
由(1)可知OB//CE,∴△AOB∽△ACE,
∴![]() ,
,
设⊙O的半径为x,则![]() ,
,
解得x=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() ;
;
(3)在Rt△AOB中AO=10-![]() =
=![]() ,cos A=
,cos A=![]() ,∴AB=5,
,∴AB=5,
在Rt△DCF中CD=![]() ,cos∠CDF=cos∠CBF=
,cos∠CDF=cos∠CBF=![]() ,∴CF=
,∴CF=![]() ,
,
∵∠A=∠CBF,∠2=∠3,
∴△ACB∽△BCF,
∴![]() =
=![]() ,
,
∴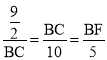 ,
,
解得,BC=![]() ,BF=
,BF=![]() .
.



科目:初中数学 来源: 题型:
【题目】问题提出:
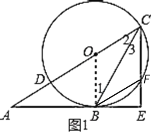
如图①菱形ABCD中,AB=4,∠ABC=60°点0是菱形ABCD两条对角线的交点,EF是经过点O的任意一条线段,容易知道线段EF将菱形ABCD的面积等分,那么线段EF的长度的最大值是 ,最小值是 。
问题探究:
如图② 四边形ABCD中,AD∥BC,AD=2,BC=4,∠B=∠C=60°,请你过点D画出将四边形ABCD面积平分的线段DE,并求出DE的长。
问题解决:
如图③.四边形ABCD是西安城区改造过程中一块不规则空地,为了美化环境,市规划办决定在这块地里种两种花弃,打算过点C修一条笔直的通道,以方便市民出行和观赏花卉,并要求通道两侧种植的花卉面积相等,经测量AB=20米,AD=100米,∠A=60°,∠ABC=150°,∠BCD=120°,若将通道记为CF,请你画出通道CF,并求出通道CF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
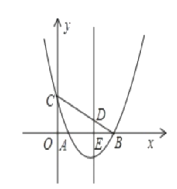
【题目】如图所示,已知抛物线![]() 与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0) ,抛物线的对称轴x=2 交x 轴于点E .
与x 轴交于A ,B 两点,与y 轴交于点C ,点B 的坐标为(3,0) ,抛物线的对称轴x=2 交x 轴于点E .
(1) 求交点A 的坐标及抛物线的函数关系式;
(2) 在平面直角坐标系xOy 中是否存在点P ,使点P 与A ,B ,C 三点构成一个平行四边形?若存在,请直接写出点P 坐标:若不存在,请说明理由;
(3) 连接CB 交抛物线对称轴于点D ,在抛物线上是否存在一点Q ,使得直线CQ 把四边形 分成面积比为1:7 的两部分?若存在,请求出点Q 坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019中国北京世界园艺博览会于2019年4月29日至10月7日在北京市延庆区举办,预售期门票价然有“平日票”和“推定日票”两种,其中平日票的单价比指定日票的单价少40元1张:某学校计划组织学生去参观,用9600元购买的平日票的票数与用12800元购买的旅定日票的票数相等.
(1)求该学校购买的平日票、指定日票的单价分别是多少元?
(2)若两种票共购买了200张,且购买的总费用是28800元,求购买了多少张平日票?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则:①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣l<x<3,其中正确的是( )
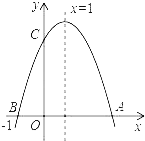
A.①②④B.②④C.①④D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x+1的图象l与y轴交于点C,A1的坐标为(1,0),点B1在直线l上,且A1B1平行于y轴,连接CA1、OB1交于点P1,过点A1作A1B2∥OB1交直线l于点B2,过点B1作B1A2∥CA1交x轴于点A2,A1B2与B1A2交于点P2,……,按此进行下去,则点P2019的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:
“读书节”活动计划书 | ||
书本类别 | A类 | B类 |
进价(单位:元) | 18 | 12 |
备注 | 1.用不超过16800元购进A,B两类图书共1000本; 2.A类图书不少于600本; …… |
(1)陈经理查看计划数时发现:A类图书的标价是B类图书标价的1.5倍,若顾客用540元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少10本,请求出A,B两类图书的标价;
(2)经市场调查后,陈经理发现他们高估了“读书节”对图书销售的影响,便调整了销售方案,A类图书每本标价降低a元(0<a<5)销售,B类图书价格不变,那么书店应如何进货才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC的边AB上一点,⊙O与半径AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.
⑴求证:∠C=90o;
⑵当BC=2,sinA=![]() 时,求AF的长.
时,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )
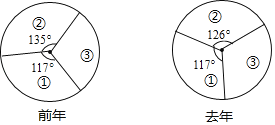
A. ①的收入去年和前年相同
B. ③的收入所占比例前年的比去年的大
C. 去年②的收入为2.8万
D. 前年年收入不止①②③三种农作物的收入
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com