
【题目】如图,点O是△ABC的边AB上一点,⊙O与半径AC相切于点E,与边BC、AB分别相交于点D、F,且DE=EF.
⑴求证:∠C=90o;
⑵当BC=2,sinA=![]() 时,求AF的长.
时,求AF的长.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图,连接OE,BE,通过对等弦、对等弧、对等圆周角以及等量转化找到∠OEB与∠DBE相等,再运用切线和平行线的定理即可解答
(2)先求出AB的长度,再通过解Rt△AOE求出半径长度,最后求出AF的长度.
解:(1)连接OE,BE,
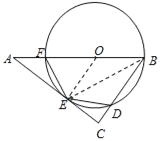
∵DE=EF,∴![]() ;
;
∴∠OBE=∠DBE.
∵OE=OB,∴∠OEB=∠OBE.
∴∠OEB=∠DBE.
∴OE∥BC.
∵⊙O与边AC相切于点E,∴OE⊥AC.
∴∠AEO=90°.
∴∠C=∠AEO=90°
(2)在△ABC,∠C=90°,BC=2,sinA=![]() ,∴AB=5.
,∴AB=5.
设⊙O的半径为r,则AO=5﹣r,
在Rt△AOE中,sinA=![]() =
=![]() ,∴r=
,∴r=![]() .
.
∴AF=5﹣2×![]() =
=![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
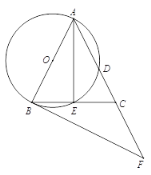
【题目】如图,在△ABC 中,AB = AC,以AB为直径的⊙O 分 别交AC,BC于点 D,E,过点B作⊙O的切线, 交 AC的延长线于点F.
(1) 求证:∠CBF =![]() ∠CAB;
∠CAB;
(2) 若CD = 2,![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
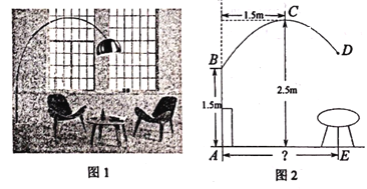
【题目】图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三张“黑桃”扑克牌,背面完全相同将三张扑克牌背面朝上,洗匀后放在桌面上甲,乙两人进行摸牌游戏,甲先从中随机抽取一张,记下数字再放回洗匀,乙再从中随机抽取一张.

(1)甲抽到“黑桃”,这一事件是 事件(填“不可能“,“随机“,“必然”);
(2)利用树状图或列表的方法,求甲乙两人抽到同一张扑克牌的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4人聚会,吗,每人带了一件礼物,4件礼物从外盒包装看完全相同,将4件礼物放在一起.
(1)甲从中随机抽取一件,则甲抽到不是自己带来的礼物的概率是 ;
(2)甲先从中随机抽取一件,不放回,乙再从中随机抽取一件,求甲、乙2人抽到的都不是自己带来的礼物的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
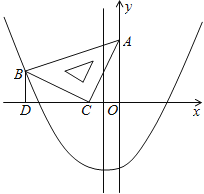
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,点C为 (-1,0).如图17所示,B点在抛物线![]() 图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
图象上,过点B作BD⊥x轴,垂足为D,且B点横坐标为-3.
(1)求证:△BDC≌△COA;
(2)求BC所在直线的函数关系式;
(3)抛物线的对称轴上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com