
【题目】问题提出:
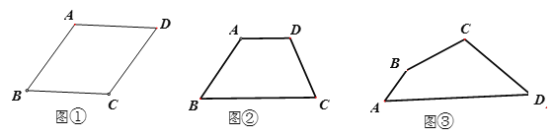
如图①菱形ABCD中,AB=4,∠ABC=60°点0是菱形ABCD两条对角线的交点,EF是经过点O的任意一条线段,容易知道线段EF将菱形ABCD的面积等分,那么线段EF的长度的最大值是 ,最小值是 。
问题探究:
如图② 四边形ABCD中,AD∥BC,AD=2,BC=4,∠B=∠C=60°,请你过点D画出将四边形ABCD面积平分的线段DE,并求出DE的长。
问题解决:
如图③.四边形ABCD是西安城区改造过程中一块不规则空地,为了美化环境,市规划办决定在这块地里种两种花弃,打算过点C修一条笔直的通道,以方便市民出行和观赏花卉,并要求通道两侧种植的花卉面积相等,经测量AB=20米,AD=100米,∠A=60°,∠ABC=150°,∠BCD=120°,若将通道记为CF,请你画出通道CF,并求出通道CF的长。
【答案】问题提出:![]() ,
,![]() ;问题探究:线段DE如图所示,DE=
;问题探究:线段DE如图所示,DE=![]() ;问题解决:通道CF如图所示,CF=35米.
;问题解决:通道CF如图所示,CF=35米.
【解析】
问题提出:由题意可知,当EF⊥AD时,EF最短,当EF与BD重合时,EF最长,然后分别求解即可;
问题探究:如图②,取AB中点F,连接DF并延长交CB延长线于点G,取CG中点E,连接DE,首先易证△AFD≌△BFG,通过作CG中点E得到S△DEG=S△DEC,即可证明DE即为所求,然后根据等腰梯形的性质和∠C=60°可求出DM,EM,最后利用勾股定理求出DE即可;
问题解决:如图③,连接AC,过点B作BH∥AC交DA延长线于点H,取DH中点F,由S△HAC= S△BAC可知S四边形ABCD=S△CHD,即可证明CF即为所求;然后如图④,延长AB,DC交于点M,过点C作CN⊥AD,根据含30°直角三角形的性质可求出CN和ND,根据三角形面积可求出DF,然后利用勾股定理求出CF即可.
解:问题提出:如图①,由题意可知,当EF⊥AD时,EF最短,
∵AB=4,∠ABC=60°,
∴△ABC是等边三角形,
∴AC=4,∠DAO=60°,
∴AO=2,
∴OE=![]() ,
,
∴EF=2OE=![]() ;
;
当EF与BD重合时,EF最长,
∵AB=4,AO=2,
∴BO=![]() ,
,
此时EF=BD=2BO=![]() ,
,
故答案为:![]() ,
,![]() ;
;
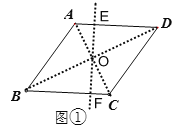
问题探究:如图②,取AB中点F,连接DF并延长交CB延长线于点G,取CG中点E,连接DE,则DE即为所求;
∵AD∥BC,
∴∠ADG=∠G,
∵∠AFD=∠BFG,AF=BF,
∴△AFD≌△BFG,
∴S△AFD= S△BFG,
∵E是CG中点,
∴S△DEG=S△DEC,
∴S四边形ABED= S△DEC,即DE将四边形ABCD面积平分,
过点D作DM⊥BC于点M,
∵AD=2,BC=4,∠B=∠C=60°,
∴CE=3,CM=1,
∴DM=![]() ,EM=2,
,EM=2,
∴DE=![]() ;
;
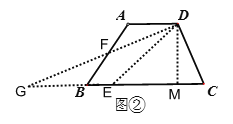
问题解决:如图③,连接AC,过点B作BH∥AC交DA延长线于点H,取DH中点F,则CF即为所求;
∵BH∥AC,
∴S△HAC= S△BAC,
∴S四边形ABCD=S△CHD,
∵F为DH中点,
∴CF将四边形ABCD面积平分;
如图④,延长AB,DC交于点M,
∵∠ABC=150°,∠BCD=120°,
∴∠MBC=30°,∠BCM=60°,
∴∠M=90°,
∵AB=20米,AD=100米,∠A=60°,
∴∠D=30°,
∴AM=50米,MD=![]() 米,
米,
∴BM=30米,MC=![]() 米,
米,
∴S△CFD=![]() S四边形ABCD=
S四边形ABCD=![]() (S△AMD-S△BMC)=
(S△AMD-S△BMC)=![]() ,
,
过点C作CN⊥AD,CD=![]() 米,
米,
∴CN=![]() 米,ND=60米,
米,ND=60米,
∴S△CFD=![]() ,
,
解得:DF=55米,
∴NF=5米,
∴CF=![]() 米.
米.




 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”.如果等腰三角形的腰长为2,“内角正度值”为![]() ,那么该三角形的面积等于___.
,那么该三角形的面积等于___.
查看答案和解析>>
科目:初中数学 来源: 题型:
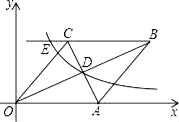
【题目】如图,已知:如图,在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=![]() (x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
(x>0)经过D点,交BC的延长线于E点,且OBAC=160,有下列四个结论:
①双曲线的解析式为y=![]() (x>0);
(x>0);
②E点的坐标是(5,8);
③sin∠COA=![]() ;
;
④AC+OB=12![]() .
.
其中正确的结论有 (填上序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB = AC,以AB为直径的⊙O 分 别交AC,BC于点 D,E,过点B作⊙O的切线, 交 AC的延长线于点F.
(1) 求证:∠CBF =![]() ∠CAB;
∠CAB;
(2) 若CD = 2,![]() ,求FC的长.
,求FC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
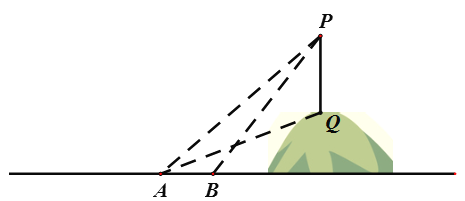
【题目】为了测量山坡上的电线杆PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为30°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是60°,求信号塔PQ得高度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两块完全相同的直角三角形纸板ABC和DEF叠放,其中∠ABC=∠DEF=90°,点O为边BC和EF的交点.
(1)求证:△BOF≌△COE.
(2)若∠F=30°,AE=1,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ACE中,∠AEC=90°,CB平分∠ACE交AE于点B,AC边上一点O,⊙O经过点B、C,与AC交于点D,与CE交于点F,连结BF。
(1)求证:AE是⊙O的切线;
(2)若![]() ,AE=8,求⊙O的半径;
,AE=8,求⊙O的半径;
(3)在(2)条件下,求BF的长。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com