
【题目】如图,在△ABC 中,AB = AC,以AB为直径的⊙O 分 别交AC,BC于点 D,E,过点B作⊙O的切线, 交 AC的延长线于点F.
(1) 求证:∠CBF =![]() ∠CAB;
∠CAB;
(2) 若CD = 2,![]() ,求FC的长.
,求FC的长.

【答案】(1)见解析;(2)FC= ![]() .
.
【解析】
(1)利用等腰三角形的性质易证∠BAE=∠EAC=![]() ∠CAB,由弦切角定理可得∠BAE=∠CBF,即可证明.
∠CAB,由弦切角定理可得∠BAE=∠CBF,即可证明.
(2)连接BD,由∠DBC=∠CBF. 得到tan∠DBC=![]() .得出BD=4. 设AB=x,则AD=
.得出BD=4. 设AB=x,则AD=![]() ,在RtΔABD中,根据勾股定理求得AB=5,证明ΔABD∽ΔAFB,根据相似三角形的性质即可求解.
,在RtΔABD中,根据勾股定理求得AB=5,证明ΔABD∽ΔAFB,根据相似三角形的性质即可求解.
(1)证明:∵AB 为⊙O的直径,
∴∠AEB=90°.
∴∠BAE+∠ABC=90°,
∵AB = AC,
∴∠BAE=∠EAC=![]() ∠CAB.
∠CAB.
∵BF为⊙O 的切线,
∴∠ABC+∠CBF=90°.
∴∠BAE=∠CBF.
∴∠CBF =![]() ∠CAB.
∠CAB.
(2)解:连接BD,
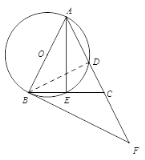
∵AB 为⊙O的直径,
∴∠ADB=90°.
∵∠DBC=∠DAE,
∴∠DBC=∠CBF.
∵tan∠CBF=![]() .
.
∴tan∠DBC=![]() .
.
∵CD=2,
∴BD=4.
设AB=x,则AD=![]() ,
,
在RtΔABD中,∠ADB=90°,由勾股定理得x=5.
∴AB=5,AD=3.
∵∠ABF=∠ADB=90°,∠BAF=∠BAF.
∴ΔABD∽ΔAFB.
∴![]() .
.
∴AF=![]() .
.
∴FC=AF-AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE =________.

查看答案和解析>>
科目:初中数学 来源: 题型:
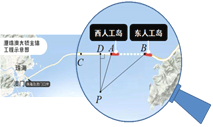
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
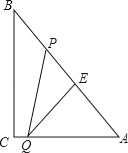
【题目】如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点,点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm,当点Q到达顶点C时,P,Q同时停止运动,设P,Q两点运动时间为t秒.
(1)当t为何值时,PQ∥BC?
(2)设四边形PQCB的面积为y,求y关于t的函数关系式;
(3)四边形PQCB面积能否是△ABC面积的![]() ?若能,求出此时t的值;若不能,请说明理由;
?若能,求出此时t的值;若不能,请说明理由;
(4)当t为何值时,△AEQ为等腰三角形?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
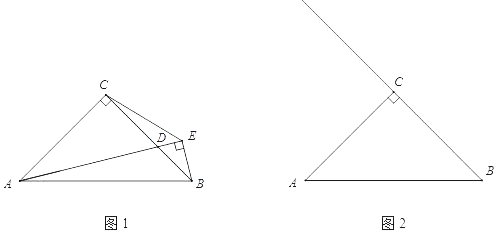
【题目】已知:Rt△ABC中,∠ACB=90°,AC=BC.
(1)如图1,点D是BC边上一点(不与点B,C重合),连接AD,过点B作BE⊥AD,交AD的延长线于点E,连接CE.若∠BAD=α,求∠DBE的大小(用含α的式子表示);
(2)如图2,点D在线段BC的延长线上时,连接AD,过点B作BE⊥AD,垂足E在线段AD上,连接CE.
①依题意补全图2;
②用等式表示线段EA,EB和EC之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
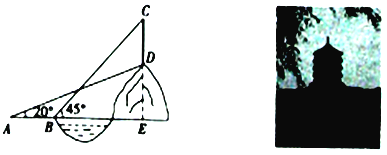
【题目】茗阳阁位于河南省信阳市狮河区茶韵路一号,建成于2007年4月29日.是一栋由多种中国建筑元素,由雕栏飞檐、勾心斗角、斗拱图腾等多种形式的中国古代建筑元素汇聚而成,具有浓郁地方古建筑特色的塔式阁楼.茗阳阁是信阳新建的城市文化与形象的代表建筑之一,同时茗阳阁旁的风景也是优美至极.某数学课外兴趣小组为了测量建在山丘![]() 上的茗阳阁
上的茗阳阁![]() 的高度,在山脚下的广场上
的高度,在山脚下的广场上![]() 处测得建筑物点
处测得建筑物点![]() (即山顶)的仰角为20°,沿水平方向前进20米到达
(即山顶)的仰角为20°,沿水平方向前进20米到达![]() 点,测得建筑物顶部
点,测得建筑物顶部![]() 点的仰角为45°,已知山丘
点的仰角为45°,已知山丘![]() 高37.69米.求塔的高度
高37.69米.求塔的高度![]() .(结果精确到1米,参考数据:
.(结果精确到1米,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
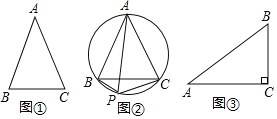
(1)已知:如图①,△ABC中请你用尺规在BC边上找一点D,使得点A到点BC的距离最短.
(2)托勒密(Ptolemy)定理指出,圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图②,P是正△ABC外接圆的劣弧BC上任一点(不与B、C重合),请你根据托勒密(Ptolemy)定理证明:PA=PB+PC
问题解决:
(3)如图③,某学校有一块两直角边长分别为30m、60m的直角三角形的草坪,现准备在草坪内放置一对石凳及垃圾箱在点P处,使P到A、B、C三点的距离之和最小,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离(结果保留根号);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一声汽笛长鸣,火车开进了蔡家崖.这是我省吕梁革命老区人民期盼已久的客运列车.蔡家崖列车的开通.带动老区驶入了发展红色旅游的快车进.某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,回答下列问题:

(1)求本次抽样调查的总人数:
(2)补全条形统计图;
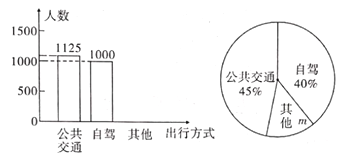
(3)扇形统计图中“其他”部分扇形的圆心角度数为____;
(4)去年“国庆”期问到吕梁观光的旅游者为275万人,则选择自驾方式出行的有多少万人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com