
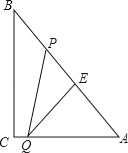
����Ŀ����ͼ��Rt��ABC�У���C��90�㣬BC��8cm��AC��6cm����P��B������BA��A�˶����ٶ�Ϊÿ��1cm����E�ǵ�B��PΪ�Գ����ĵĶԳƵ㣬��P�˶���ͬʱ����Q��A������AC��C�˶����ٶ�Ϊÿ��2cm������Q���ﶥ��Cʱ��P��Qͬʱֹͣ�˶�����P��Q�����˶�ʱ��Ϊt�룮
(1)��tΪ��ֵʱ��PQ��BC��
(2)���ı���PQCB�����Ϊy����y����t�ĺ�����ϵʽ��
(3)�ı���PQCB����ܷ��ǡ�ABC�����![]() �����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
�����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
(4)��tΪ��ֵʱ����AEQΪ���������Σ���ֱ��д�������
���𰸡�(1)t��![]() ��(2)y��
��(2)y��![]() t2��8t+24��(3)�ı���PQCB������ǡ�ABC�����
t2��8t+24��(3)�ı���PQCB������ǡ�ABC�����![]() ����ʱt��ֵΪ5��
����ʱt��ֵΪ5��![]() ��(4)��tΪ
��(4)��tΪ![]() ��
��![]() ��
��![]() ��ʱ����AEQΪ���������Σ�
��ʱ����AEQΪ���������Σ�
��������
���⣨1������Rt��ABC�У��ɹ��ɶ������AB=10������BP=t��AQ=2t���ó�AP=10-t��Ȼ����PQ��BC������ƽ���߷��߶γɱ��������ó�![]() ���г�����ʽ
���г�����ʽ![]() ����⼴�ɣ�
����⼴�ɣ�
��2������S�ı���PQCB=S��ACB-S��APQ=![]() ACBC-
ACBC-![]() APAQsinA�����ɵó�y����t�ĺ�����ϵʽ��
APAQsinA�����ɵó�y����t�ĺ�����ϵʽ��
��3�������ı���PQCB�������ABC�����![]() ���г�����
�������![]() t2-8t+24=
t2-8t+24=![]() ��24���ⷽ�̼��ɣ�
��24���ⷽ�̼��ɣ�
��4����AEQΪ����������ʱ��������������ۣ���AE=AQ����EA=EQ����QA=QE��ÿһ������������г�����t�ķ��̣��ⷽ�̼��ɣ�
�����������1��Rt��ABC�У��ߡ�C=90����BC=8cm��AC=6cm��
��AB=10cm��
��BP=t��AQ=2t��
��AP=AB-BP=10-t��
��PQ��BC��
��![]() ��
��
��![]() ��
��
���t=![]() ��
��
��2����S�ı���PQCB=S��ACB-S��APQ=![]() ACBC-
ACBC-![]() APAQsinA
APAQsinA
��y=![]() ��6��8-
��6��8-![]() ����10-2t��2t
����10-2t��2t![]() =24-
=24-![]() t��10-2t��=
t��10-2t��=![]() t2-8t+24��
t2-8t+24��
��y����t�ĺ�����ϵʽΪy=![]() t2-8t+24��
t2-8t+24��
��3���ı���PQCB���������ABC�����![]() ���������£�
���������£�
�����⣬��
![]() t2-8t+24=
t2-8t+24=![]() ��24��
��24��
��������t2-10t+12=0��
���t1=5-![]() ��t2=5+
��t2=5+![]() ������������ȥ����
������������ȥ����
���ı���PQCB���������ABC�����![]() ����ʱt��ֵΪ5-
����ʱt��ֵΪ5-![]() ��
��
��4����AEQΪ����������ʱ��������������ۣ�
�����AE=AQ����ô10-2t=2t�����t=![]() ��
��
�����EA=EQ����ô��10-2t����![]() =t�����t=
=t�����t=![]() ��
��
�����QA=QE����ô2t��![]() =5-t�����t=
=5-t�����t=![]() ��
��
�ʵ�tΪ![]() �롢
�롢![]() �롢
�롢![]() ��ʱ����AEQΪ���������Σ�
��ʱ����AEQΪ���������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
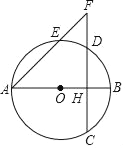
����Ŀ����ͼ����֪AB��ԲO��ֱ������CD��AB������H�ڰ뾶OB�ϣ�AH=5��CD=![]() ����E�ڻ�AD�ϣ�����AE��CD���ӳ��߽��ڵ�F��
����E�ڻ�AD�ϣ�����AE��CD���ӳ��߽��ڵ�F��
��1����ԲO�İ뾶��
��2�����AE=6����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����õ��������ķ��Ȳ���ʹ����PTC���Ȳ��ϣ����ĵ���R��k�������¶�t����������һ����Χ�ڣ��仯�Ĵ���ͼ����ͼ��ʾ��ͨ����Ȳ��ϵ��¶���������10��������30���Ĺ����У��������¶ȳɷ�������ϵ�������¶ȴﵽ30��ʱ�������½�����Сֵ�����������¶����߶����ӣ��¶�ÿ����1������������![]() k����
k����
��1����10��t��30ʱ��R��t֮��Ĺ�ϵʽ��
��2�����¶���30��ʱ����R��ֵ�������t��30ʱ��R��t֮��Ĺ�ϵʽ��
��3�����õ���������ʹ�ù����У��¶���ʲô��Χ��ʱ�����Ȳ��ϵĵ��費����6 k����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ����ABC�ڽ�����O��AB=AC��BDΪ��O���ң���AB��CD������A����O������AE��DC���ӳ��߽��ڵ�E��AD��BC���ڵ�F��

��1����֤���ı���ABCE��ƽ���ı��Σ�
��2����AE=6��CD=5����OF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ơ������������˻�������ѧ�о�������˻�����������ʾ�����˻�A�����CD�ľ���Ϊ420�ף������˻��ײ�A���������ϴ����ס���֣�ݻ�չ����ǧ�����ģ�����B�ĸ���Ϊ30�㣬���ⶰ��¥�ײ�C�ĸ���Ϊ60�㣬���ϴ����ס��ĸ߶ȣ���![]() ��
��![]() ��
��![]() ��2.236�������ȷ��1m����
��2.236�������ȷ��1m����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ�����ͼ����x�ύ��A����3��0����B��1��0�����㣬��y���ڵ�C��0��3������C��D�Ƕ��κ���ͼ���ϵ�һ�ԶԳƵ㣬һ�κ�����ͼ�����B��D��

��1������κ����Ľ���ʽ��
��2������ͼ��ֱ��д��ʹһ�κ���ֵ���ڶ��κ���ֵ��x��ȡֵ��Χ��
��3����ֱ����y��Ľ���ΪE������AD��AE������ADE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӻ���ij��ѧ������1������ѧ��ȤС��Ϊ�˽�ȫУ800������ѧ���ġ����б�ҵѡ����ѧ�;�ҵ��������ضԱ���50��ͬѧ�ǽ��е��飬����ȫ��ͬѧ�����3����Ҫ�۵㣺A���У�B�м���C��ҵ�������˵��飨Ҫ��ÿλͬѧֻѡ�Լ����Ͽɵ�һ��۵㣩�����Ƴ�������ͳ��ͼ����ͼ������ش��������⣺
��1���ð�ѧ��ѡ���� ���۵��������࣬������ ���ˣ�������ͳ��ͼ�У��ù۵��������������Բ�Ľ����� ���ȣ�
��2�������������Ƹ�У����ѧ��ѡ���м����۵��������
��3����֪�ð�ֻ��2λŮͬѧѡ��ҵ���۵㣬��������δӸù۵��У����ѡȡ2λͬѧ���е��飬��ôǡ��ѡ����2λŮͬѧ�ĸ����Ƕ��٣���������ͼ���б���������𣩣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У���OΪԭ�㣬��A������Ϊ��0��8������C������Ϊ��6��0����������y����![]() x2+bx+c������A��C����AB���ڵ�D��
x2+bx+c������A��C����AB���ڵ�D��
��1���������ߵĺ�������ʽ��
��2����PΪ�߶�BC��һ�����㣨�����C�غϣ�����QΪ�߶�AC��һ�����㣬AQ��CP������PQ����CP��m����CPQ�����ΪS��
����S����m�ĺ�������ʽ��
�ڵ�S���ʱ����������y����![]() x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ȫ����������ʵʩ����������������ͥ�������ԵĹ滮.����������Ů�ĸ�����ͬ���ش�����������
��1������ͥ����һ���к���������һ�����ӣ����ڶ���������Ů���������� ��
��2���Ҽ�ͥû�к���������������������������һ��������Ů��������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com