
����Ŀ���ӻ���ij��ѧ������1������ѧ��ȤС��Ϊ�˽�ȫУ800������ѧ���ġ����б�ҵѡ����ѧ�;�ҵ��������ضԱ���50��ͬѧ�ǽ��е��飬����ȫ��ͬѧ�����3����Ҫ�۵㣺A���У�B�м���C��ҵ�������˵��飨Ҫ��ÿλͬѧֻѡ�Լ����Ͽɵ�һ��۵㣩�����Ƴ�������ͳ��ͼ����ͼ������ش��������⣺
��1���ð�ѧ��ѡ���� ���۵��������࣬������ ���ˣ�������ͳ��ͼ�У��ù۵��������������Բ�Ľ����� ���ȣ�
��2�������������Ƹ�У����ѧ��ѡ���м����۵��������
��3����֪�ð�ֻ��2λŮͬѧѡ��ҵ���۵㣬��������δӸù۵��У����ѡȡ2λͬѧ���е��飬��ôǡ��ѡ����2λŮͬѧ�ĸ����Ƕ��٣���������ͼ���б���������𣩣�

���𰸡���1��A���й۵㣮30�� 216����2��256�ˣ���3��![]() ��
��
��������
���⣨1��ȫ����������ѡ����A�������۵�İٷֱȼ��ɵõ�ѡ����A�������۵����������360������ѡ����A�������۵�İٷֱȼ��ɵõ�ѡ����A�������Ĺ۵��������������Բ�ĽǵĶ�����
��2����ȫУ�����꼶ѧ��������ѡ����B�м����۵�İٷֱȼ��ɹ��Ƹ�У����ѧ��ѡ�����м����۵��������
��3���ȼ�����ð�ѡ������ҵ���۵������Ϊ4�ˣ�����ж���2λŮͬѧ��2λ����ѡ������ҵ���۵㣬���б�չʾ12�ֵȿ��ܵĽ�������ҳ�����2Ů�Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
�����������1���ð�ѧ��ѡ��A���й۵��������࣬����60%��50=30���ˣ���������ͳ��ͼ�У��ù۵��������������Բ�Ľ���60%��360��=216����
��2����800��32%=256���ˣ���
�����Ƹ�У����ѧ��ѡ�����м����۵������Լ��256�ˣ�
��3���ð�ѡ������ҵ���۵������=50����1-60%-32%��=50��8%=4���ˣ�����ð���2λŮͬѧ��2λ����ѡ������ҵ���۵㣬
�б����£�
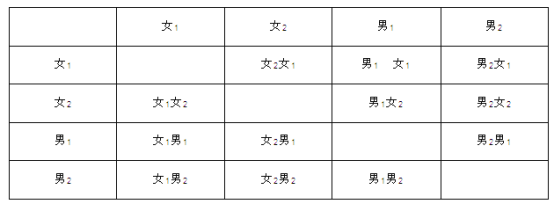
����12�ֵȿ��ܵĽ���������г���2Ů���������2�֣�
����ǡ��ѡ��2λŮͬѧ�ĸ���=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���ʦΪ�˽�Ůѧ������Ͷ��������������ȡ8��Ů������ÿ��4�ζ���Ͷ���IJ��ԣ���������ͳ����ͼ��ʾ��

��1����Ů����������ƽ��������λ����
��2��Ͷ��4�Σ�����3�����ϣ���3����Ϊ���㣬ȫУ��Ů��1200�ˣ�����Ϊ�����㡱�ȼ���Ů��ԼΪ�����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2+bx+c��ͼ���㣨4��3������3��0����
��1����b��c��ֵ��
��2������ö��κ���ͼ��Ķ�������ͶԳ��ᣬ������������ϵ�л����ú�����ͼ����
��3���ú�����ͼ��������ƽ�Ƶõ�y=x2��ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
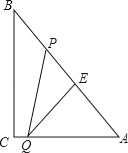
����Ŀ����ͼ��Rt��ABC�У���C��90�㣬BC��8cm��AC��6cm����P��B������BA��A�˶����ٶ�Ϊÿ��1cm����E�ǵ�B��PΪ�Գ����ĵĶԳƵ㣬��P�˶���ͬʱ����Q��A������AC��C�˶����ٶ�Ϊÿ��2cm������Q���ﶥ��Cʱ��P��Qͬʱֹͣ�˶�����P��Q�����˶�ʱ��Ϊt�룮
(1)��tΪ��ֵʱ��PQ��BC��
(2)���ı���PQCB�����Ϊy����y����t�ĺ�����ϵʽ��
(3)�ı���PQCB����ܷ��ǡ�ABC�����![]() �����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
�����ܣ������ʱt��ֵ�������ܣ���˵�����ɣ�
(4)��tΪ��ֵʱ����AEQΪ���������Σ���ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ˡ������������У�������������������ij������Ͻ���ڵ�һ�����Ϊ1000m2�Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի������ֲݲ��ֵ����Ϊ![]() ��m2�����ֲ��������
��m2�����ֲ��������![]() 1��Ԫ����
1��Ԫ����![]() ��m2���ĺ�����ϵʽΪ
��m2���ĺ�����ϵʽΪ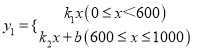 ����ͼ����ͼ��ʾ���Ի��������
����ͼ����ͼ��ʾ���Ի��������![]() 2��Ԫ����x��m2���ĺ�����ϵʽΪ
2��Ԫ����x��m2���ĺ�����ϵʽΪ![]() 2=��0.01
2=��0.01![]() 2��20
2��20![]() +30000��0��
+30000��0��![]() ��1000����
��1000����
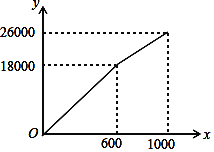
��1����ֱ��д��k1��k2��b��ֵ��
��2�������1000m2�յص��̻��ܷ���ΪW��Ԫ����������W��![]() �ĺ�����ϵʽ������̻��ܷ���W�����ֵ��
�ĺ�����ϵʽ������̻��ܷ���W�����ֵ��
��3�����ֲݲ��ֵ����������700m2���Ի����ֵ����������100m2��������̻��ܷ���W����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��50Ԫ�����ۼ�Ϊÿ��70Ԫʱ��ÿ���ڿ�����300�������轵�۴������Ҿ��г����飺ÿ����1Ԫ��ÿ���ڿɶ�����20������ȷ��ӯ����ǰ���£�����������⣺
��1������ÿ������xԪ��ÿ�����۳���Ʒ������ΪyԪ����д��y��x�ĺ�����ϵʽ��������Ա���x��ȡֵ��Χ��
��2�������۶���Ԫʱ��ÿ���ڵ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
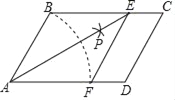
����Ŀ����ͼ����ABCD�У��Ե�4ΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BF�ij�Ϊ�뾶�������������ڵ�P������AP��͢����BC�ڵ�E������EF
BF�ij�Ϊ�뾶�������������ڵ�P������AP��͢����BC�ڵ�E������EF
��1���������ϳ߹���ͼ�Ĺ��̣���֤���ı���ABEF�����Σ�
��2����AB��2��AE��2![]() �����BAD�Ĵ�С��
�����BAD�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(9��)��֪��![]() ABCD������AB��AD�ij��ǹ���x�ķ���
ABCD������AB��AD�ij��ǹ���x�ķ���![]() ������ʵ������
������ʵ������
��1����mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
��2����AB�ij�Ϊ2����ô![]() ABCD���ܳ��Ƕ��٣�
ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
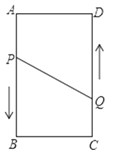
����Ŀ����ͼ��A��B��C��DΪ���ε��ĸ�������AB=16cm��AD=6cm������P��Q�ֱ�ӵ�A��Cͬʱ��������P��3cm/s���ٶ����B�ƶ���һֱ����BΪֹ����Q��2 cm/s���ٶ���D�ƶ���
��1��P��Q����ӳ�����ʼ�����룿�ı���PBCQ�����Ϊ33cm2��
��2��P��Q����ӳ�����ʼ������ʱ����P�͵�Q�ľ�����10cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com