
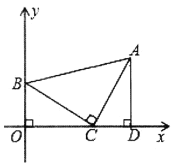
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x+8;(2)①S=﹣
x+8;(2)①S=﹣![]() m2+3m;②满足条件的点F共有四个,坐标分别为F1(
m2+3m;②满足条件的点F共有四个,坐标分别为F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ).
).
【解析】
(1)将A、C两点坐标代入抛物线y=-![]() x2+bx+c,即可求得抛物线的解析式;
x2+bx+c,即可求得抛物线的解析式;
(2)①先用m表示出QE的长度,进而求出三角形的面积S关于m的函数;
②直接写出满足条件的F点的坐标即可,注意不要漏写.
解:(1)将A、C两点坐标代入抛物线,得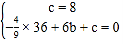 ,
,
解得:![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8;
x+8;
(2)①∵OA=8,OC=6,
∴AC=![]() =10,
=10,
过点Q作QE⊥BC与E点,则sin∠ACB = ![]() =
= ![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QE=![]() (10﹣m),
(10﹣m),
∴S=![]() CPQE=
CPQE=![]() m
m![]() ×(10﹣m)=﹣
×(10﹣m)=﹣![]() m2+3m;
m2+3m;
②∵S=![]() CPQE=
CPQE=![]() m×
m×![]() (10﹣m)=﹣
(10﹣m)=﹣![]() m2+3m=﹣
m2+3m=﹣![]() (m﹣5)2+
(m﹣5)2+![]() ,
,
∴当m=5时,S取最大值;
在抛物线对称轴l上存在点F,使△FDQ为直角三角形,
∵抛物线的解析式为y=﹣![]() x2+
x2+![]() x+8的对称轴为x=
x+8的对称轴为x=![]() ,
,
D的坐标为(3,8),Q(3,4),
当∠FDQ=90°时,F1(![]() ,8),
,8),
当∠FQD=90°时,则F2(![]() ,4),
,4),
当∠DFQ=90°时,设F(![]() ,n),
,n),
则FD2+FQ2=DQ2,
即![]() +(8﹣n)2+
+(8﹣n)2+![]() +(n﹣4)2=16,
+(n﹣4)2=16,
解得:n=6±![]() ,
,
∴F3(![]() ,6+
,6+![]() ),F4(
),F4(![]() ,6﹣
,6﹣![]() ),
),
满足条件的点F共有四个,坐标分别为
F1(![]() ,8),F2(
,8),F2(![]() ,4),F3(
,4),F3(![]() ,6+
,6+![]() ),F4(
),F4(![]()
![]() ).
).


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:初中数学 来源: 题型:
【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买商品共花去了
![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)试验,她们共做了60次试验,试验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.
(2)小颖说:“根据上述试验,一次试验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,等腰直角![]() 中,
中,![]() ,
,![]() ,现将该三角形放置在平面直角坐标系中,点
,现将该三角形放置在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .
.
(1)过点![]() 作
作![]() 轴,求
轴,求![]() 的长及点
的长及点![]() 的坐标;
的坐标;
(2)连接![]() ,若
,若![]() 为坐标平面内异于点
为坐标平面内异于点![]() 的点,且以
的点,且以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出满足条件的点
全等,请直接写出满足条件的点![]() 的坐标;
的坐标;
(3)已知![]() ,试探究在
,试探究在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?若存在,请直接写出点
为腰的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(个) | 100 | 80 | 60 | … |
(1)求y与x之间的函数表达式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数表达式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,测量人员在山脚A处测得山顶B的仰角为45°,沿着仰角为30°的山坡前进1000米到达D处,在D处测得山顶B的仰角为60°,求山的高度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC.
(Ⅰ)如图①,若∠P=20°,求∠BCO的度数;
(Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE= ![]() CD,求∠P的度数.
CD,求∠P的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com