
����Ŀ��ij�̳�����һ����Ʒ������Ϊÿ��20Ԫ���涨ÿ����Ʒ�ۼ۲����ڽ��ۣ��Ҳ�����60Ԫ�������鷢�֣�ÿ���������y��������ÿ����Ʒ���ۼ�x��Ԫ������һ�κ�����ϵ���䲿������������ʾ��
ÿ����Ʒ���ۼ�x��Ԫ�� | �� | 30 | 40 | 50 | �� |
ÿ���������y������ | 100 | 80 | 60 | �� |
��1����y��x֮��ĺ�������ʽ��
��2�����̳�ÿ���õ�������Ϊw��Ԫ������w��x֮��ĺ�������ʽ��
��3���������������أ�����Ʒ���ۼ�Ϊ����Ԫʱ���̳�ÿ���õ������������������Ƕ��٣�
���𰸡���1��y=-2x+160����2��w=-2x2+200x-3200����3������Ʒ���ۼ�Ϊ50Ԫʱ���̳�ÿ���õ�������������������1800��
��������
ÿ���������y(��)��ÿ����Ʒ���ۼ�x(Ԫ)����һ�κ�����ϵ���ô���ϵ������⣻
��������ı���ʽ������=�ۼ�-������⣻
���ݣ�2���ı���ʽ�Ƕ��κ��������ö��κ�������ֵ���.
��1����y��x֮��ĺ�������ʽΪy=kx+b��
��![]() ��
��
���![]() ��
��
��y��x֮��ĺ�������ʽ��y=-2x+160��
��2��������ɵã�w=��x-20����-2x+160��=-2x2+200x-3200��
��w��x֮��ĺ�������ʽ��w=-2x2+200x-3200��
��3����w=-2x2+200x-3200=-2��x-50��2+1800��20��x��60��
�൱20��x��50ʱ��w��x�����������
��50��x��60ʱ��w��x���������С��
��x=50ʱ��wȡ�����ֵ����ʱw=1800Ԫ
������Ʒ���ۼ�Ϊ50Ԫʱ���̳�ÿ���õ�������������������1800��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �ǻ�
�ǻ�![]() ������
������![]() ��
��![]() �������㣬
�������㣬![]() �ǻ�
�ǻ�![]() ��һ���㣬
��һ���㣬![]() �Ľ�ƽ���߽�
�Ľ�ƽ���߽�![]() �ڵ�
�ڵ�![]() ��
��![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ������
������![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ʱ����
ʱ����![]() ��
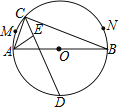
��![]() ������˶�·�����ı��ǣ� ��
������˶�·�����ı��ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ͨ�������յ������ڣ���ֱ�����ڵ���������2.1 m����Ӱ����ͼ��ʾ����֪�����Ӱ��DE�ĵ�E������ǽ�ŵľ���CE=3.9 m�����ڵױ������ľ���BC=1.2 m�����ڵĸ߶ȣ���AB��ֵ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У���OΪԭ�㣬��A������Ϊ��0��8������C������Ϊ��6��0����������y����![]() x2+bx+c������A��C����AB���ڵ�D��
x2+bx+c������A��C����AB���ڵ�D��
��1���������ߵĺ�������ʽ��
��2����PΪ�߶�BC��һ�����㣨�����C�غϣ�����QΪ�߶�AC��һ�����㣬AQ��CP������PQ����CP��m����CPQ�����ΪS��
����S����m�ĺ�������ʽ��
�ڵ�S���ʱ����������y����![]() x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�
x2+bx+c�ĶԳ���l�ϣ������ڵ�F��ʹ��DFQΪֱ�������Σ���ֱ��д�����з��������ĵ�F�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=kx��1��ͼ����P����y��ֵ��xֵ��������������P���������Ϊ��������
A. ����5��3�� B. ��1����3�� C. ��2��2�� D. ��5����1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
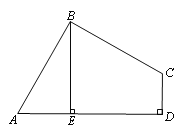
����Ŀ����֪����ͼ�����ı���ABCD�У���ABC��90����CD��AD��AD2��CD2��2AB2��
��1����֤��AB��BC��
��2����BE��AD��Eʱ����֤����BE��AE��CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֳ�ѧϰ������ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ��
��![]() ��
��![]() ������������ε������С��ͬѧ�ڽ�������ʱ���Ȼ�һ������������ÿ��С�����εı߳�Ϊ1�������������л��������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ��������������ABC�ĸߣ�������������ܼ����������������ַ���������ͼ����
������������ε������С��ͬѧ�ڽ�������ʱ���Ȼ�һ������������ÿ��С�����εı߳�Ϊ1�������������л��������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ��������������ABC�ĸߣ�������������ܼ����������������ַ���������ͼ����
��1����ABC���������_________����
��2������DEF���ߵij��ֱ�Ϊ![]() ��
��![]() ��
��![]() ������ͼ1�������������л�����Ӧ����DEF�������ù�ͼ��������������
������ͼ1�������������л�����Ӧ����DEF�������ù�ͼ��������������
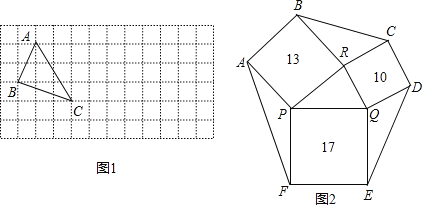
��3����ͼ2��һ�������εĻ�̳���ָ��7�����֣�����������PRBA��RQDC��QPFE������ֱ�Ϊ13��10��17������PQR����BCR����DEQ����AFP�������ȣ��������λ�̳ABCDEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������и�������������x��y������y��x�ĺ�������
�� x�������εı߳���y����������ε������
�� x�Ǿ��ε�һ�߳���y��������ε��ܳ���
�� x��һ��������y�����������ƽ������
�� x��һ��������y���������������ƽ������
A. �٢ڢ�B. �٢ڢ�C. �ڢ�D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���������ϵ�У� ��![]() ��
��![]() ���㣬 ����
���㣬 ����![]() ����ȡһ��
����ȡһ��![]() �� ʹ��
�� ʹ��![]() ����
����![]() �͵�
�͵�![]() �ľ���֮����С�����
�ľ���֮����С�����![]() ��������__________��
��������__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com