
【题目】如图,在正方形ABCD中,G是BC上任意一点,连接AG,DE⊥AG于E,BF∥DE交AG于F,探究线段AF、BF、EF三者之间的数量关系,并说明理由.

【答案】AF=BF+EF,理由见试题解析.
【解析】
试题分析:根据正方形的性质,可得AB=AD,∠DAB=∠ABC=90°,根据余角的性质,可得∠ADE=∠BAF,根据全等三角形的判定与性质,可得BF与AE的关系,再根据等量代换,可得答案.
试题解析:线段AF、BF、EF三者之间的数量关系AF=BF+EF,理由如下:
∵四边形ABCD是正方形,∴AB=AD,∠DAB=∠ABC=90°,∵DE⊥AG于E,BF∥DE交AG于F,∴∠AED=∠DEF=∠AFB=90°,∴∠ADE+∠DAE=90°,∠DAE+∠BAF=90°,∴∠ADE=∠BAF,在△ABF和△DAE中,∵∠BAF=∠ADE,∠AFB=∠DEA,AB=AD,∴△ABF≌△DAE (AAS),∴BF=AE,∵AF=AE+EF,AF=BF+EF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】![]() 与
与 ![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.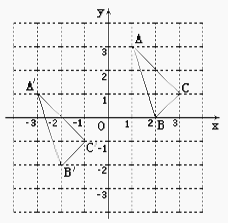
(1)分别写出下列各点的坐标:![]() ,
, ![]() ,
, ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:;
经过怎样的平移得到:;
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的对应点
内的对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
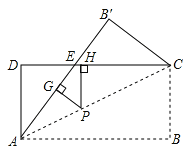
(1)试找出一个与△AED全等的三角形,并加以证明.
(2)若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,1)与点A′(5,b)关于坐标原点对称,则实数a、b的值是( )
A.a=5,b=1
B.a=﹣5,b=1
C.a=5,b=﹣1
D.a=﹣5,b=﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com