
【题目】综合与探究
如图,等腰直角![]() 中,
中,![]() ,
,![]() ,现将该三角形放置在平面直角坐标系中,点
,现将该三角形放置在平面直角坐标系中,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .
.
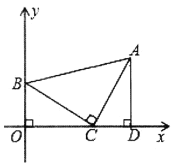
(1)过点![]() 作
作![]() 轴,求
轴,求![]() 的长及点
的长及点![]() 的坐标;
的坐标;
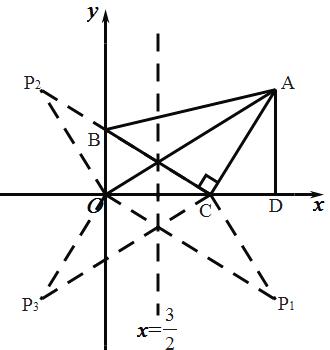
(2)连接![]() ,若
,若![]() 为坐标平面内异于点
为坐标平面内异于点![]() 的点,且以
的点,且以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 全等,请直接写出满足条件的点
全等,请直接写出满足条件的点![]() 的坐标;
的坐标;
(3)已知![]() ,试探究在
,试探究在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?若存在,请直接写出点
为腰的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)4,![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)先根据![]() 证明
证明![]() ,然后根据全等三角形的性质得出
,然后根据全等三角形的性质得出![]() 、
、![]() 的长即可得出点
的长即可得出点![]() 的坐标;
的坐标;
(2)做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ;做
;做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ;做
;做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ,根据对称图形的性质即可知道所作的图形全等,即可写出点
,根据对称图形的性质即可知道所作的图形全等,即可写出点![]() 的坐标;
的坐标;
(3)当以点![]() 为顶点时有一个点符合,当以点
为顶点时有一个点符合,当以点![]() 为顶点时分钝角三角形和锐角三角形即可求解.
为顶点时分钝角三角形和锐角三角形即可求解.
(1)∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]()
∴![]()
∵![]()
∴![]()
∵![]() 轴
轴
∴![]()
∴![]()
∴![]()
又∵![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴ 点![]() 的坐标为
的坐标为![]()
(2)①做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ,
,
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
②∵点![]() 和点
和点![]() 关于
关于![]() 对称
对称
∴做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
③做![]() 关于
关于![]() 轴的对称图形得到
轴的对称图形得到![]() ,
,
∴![]()
∴![]()
∴点![]() 的坐标为
的坐标为![]()
∴综上所述点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() ;
;
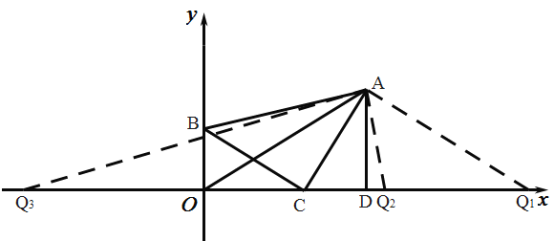
(3)①当以点![]() 为顶点时,且
为顶点时,且![]() 是腰
是腰
∵![]() 轴
轴
∴可以做点![]() 关于
关于![]() 的对称点
的对称点![]()
∴点![]() 的坐标为
的坐标为![]()
∴![]() 是
是![]() 的垂直平分线
的垂直平分线
∴![]()
∴![]() 是以
是以![]() 为腰的等腰三角形;
为腰的等腰三角形;
②当以点![]() 为顶点时,且
为顶点时,且![]() 是腰,形成锐角三角形时,
是腰,形成锐角三角形时,
即![]()
∴点![]() 的坐标为
的坐标为![]() ;
;
②当以点![]() 为顶点时,且
为顶点时,且![]() 是腰,形成钝角三角形时,
是腰,形成钝角三角形时,
即![]()
∴点![]() 的坐标为
的坐标为![]()
∴综上所述点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
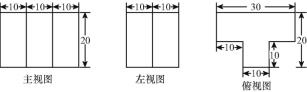
【题目】下列给出了某种工件的三视图,某工厂要铸造5000件这种铁质工件,要用去多少生铁?工件铸成后,表面需得涂一层防锈漆,已知1 kg防锈漆可以涂4 m2的铁器面,涂完这批工件要用多少防锈漆?(铁的比重为7.8 g/cm3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图点E,F分别是矩形ABCD的边AD,AB上一点,若AE=DC=2ED,且EF⊥EC.
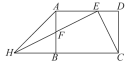
(1)求证:点F为AB的中点.
(2)延长EF与CB的延长线相交于点H,连接AH,已知ED=2,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可在甲,乙两个商店买到,已知两个商店的标价都是每本1元.但甲商店的优惠条件是:购买10本以上,从第11本开始按标价七折卖;乙商店的优惠条件是:从第1本开始就按标价的八五折卖.若小明购买练习本数量为![]() 本,在甲商店购买后的总费用为
本,在甲商店购买后的总费用为![]() 元,在乙商店购买后的总费用为
元,在乙商店购买后的总费用为![]() 元.
元.
(1)写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(2)小明要买20本练习本,到哪个商店购买较省钱?
(3)小明现有24元,最多可买多少本练习本?
查看答案和解析>>
科目:初中数学 来源: 题型:
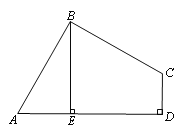
【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
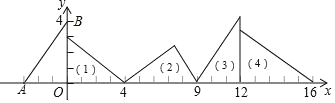
【题目】如图,在直角坐标系中,已知点 A(﹣3,0),B(0,4),对△OAB 连续作旋转变换,依次得到三角形(1),(2),(3),(4)…,则三角形(2019)的直角顶点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com