
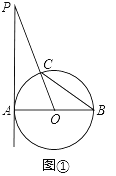
【题目】如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC.
(Ⅰ)如图①,若∠P=20°,求∠BCO的度数;
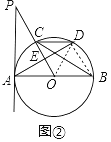
(Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE= ![]() CD,求∠P的度数.
CD,求∠P的度数.

【答案】(Ⅰ)35°(Ⅱ)30°
【解析】
(1)由PA是⊙O的切线,推出OA⊥AP,推出∠AOC=90°-20°=70°,由∠B= ![]() ∠AOC=35°,OB=OC,即可推出∠B=∠OCB=35°;
∠AOC=35°,OB=OC,即可推出∠B=∠OCB=35°;
(2)如图2中,连接BD、OD.只要证明![]() =
=![]() =
=![]() ,即可推出∠AOC=∠COD=∠BOD=60°,由PA是⊙O的切线,推出∠PAO=90°,推出∠P=30°;
,即可推出∠AOC=∠COD=∠BOD=60°,由PA是⊙O的切线,推出∠PAO=90°,推出∠P=30°;
(Ⅰ)如图1中,
∵PA是⊙O的切线,
∴OA⊥AP,
∴∠PAO=90°,∵∠P=20°,
∴∠AOC=90°﹣20°=70°,
∴∠B= ![]() ∠AOC=35°,
∠AOC=35°,
∵OB=OC,
∴∠B=∠OCB=35°,
∴∠BCO=35°.
(Ⅱ)如图2中,连接BD、OD.
∵AD⊥OP于E,
∴AE=ED, ![]() =
= ![]() ,
,
∵AE=ED,OA=OB,
∴OE= ![]() DB,
DB,
∵OE= ![]() CD,
CD,
∴CD=DB,
∴![]() =
=![]() ,
,
∴ ![]() =
=![]() =
=![]() ,
,
∴∠AOC=∠COD=∠BOD=60°,
∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠P=30°


科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面各问题中给出的两个变量x,y,其中y是x的函数的是
① x是正方形的边长,y是这个正方形的面积;
② x是矩形的一边长,y是这个矩形的周长;
③ x是一个正数,y是这个正数的平方根;
④ x是一个正数,y是这个正数的算术平方根.
A. ①②③B. ①②④C. ②④D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 过点
过点![]() ,直线
,直线![]() :
:![]() 与直线
与直线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
① 当b=4时,直接写出△OBC内的整点个数;
②若△OBC内的整点个数恰有4个,结合图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是半径为![]() cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
cm的⊙O外一点,PA,PB分别和⊙O切于点A,B,PA=PB=3cm,∠APB=60°,C是弧AB上一点,过C作⊙O的切线交PA,PB于点D,E.
(1)求△PDE的周长;
(2)若DE=![]() cm,求图中阴影部分的面积.
cm,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置教师办公桌椅A、B两型共200套,已知2套A型桌椅和1套B型桌椅共需2000元,1套A型桌椅和3套B型桌椅共需3000元.
(1)求A,B两型桌椅的单价;
(2)若需要A型桌椅不少于120套,B型桌椅不少于70套,平均每套桌椅需要运费10元.设购买A型桌椅x套时,总费用为y元,求y与x的函数关系式,并直接写出x的取值范围;
(3)求出总费用最少的购置方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,0),B(0,2),C(-4,2),若以A,B,C,D为顶点的四边形是平行四边形,则点D的坐标为________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com