【题目】如图，在矩形
中，
，
，
为
边上一点，将
沿
翻折，点
落在点
处，当
为直角三角形时，
________.
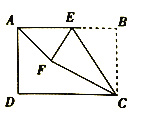
【答案】3或6
【解析】
对直角
中那个角是直角分三种情况讨论，再由折叠的性质和勾股定理可BE的长.
解：如图，若∠AEF=90°
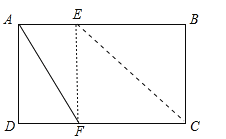
∵∠B=∠BCD=90°=∠AEF
∴四边形BCFE是矩形
∵将ABEC沿着CE翻折
∴CB=CF
∵四边形BCFE是正方形
∴BE=BC-AD=6，
如图，若∠AFE=90°
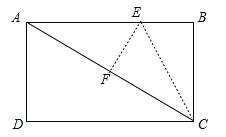
∵将△BEC沿着CE翻折
∴CB=CF=6，∠B=∠EFC=90°，BE=EF
∵∠AFE+∠EFC=180°
∴点A，点F，点C三点共线
∴
∴AF=AC-CF=4
∵
∴
∴BE=3，
若∠EAF=90°，
∵CD=8> CF=6
∴点F不可能落在直线AD上
∴.不存在∠EAF=90
综上所述：BE=3或6
故答案为：3或6
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，PA切⊙O于A，OP交⊙O于C，连接BC．
（Ⅰ）如图①，若∠P=20°，求∠BCO的度数；
（Ⅱ）如图②，过A作弦AD⊥OP于E，连接DC，若OE= 
CD，求∠P的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，
与
都是等腰直角三角形，直角边
，
在同一条直线上，点
、
分别是斜边
、
的中点，点
为
的中点，连接
，
，
，
，
．
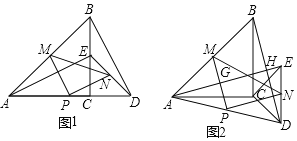
（1）观察猜想：
图1中，与的数量关系是______，位置关系是______．
（2）探究证明：
将图1中的绕着点
顺时针旋转
（
），得到图2，与
、分别交于点
、
，请判断（1）中的结论是否成立，若成立，请证明；若不成立，请说明理由．
（3）拓展延伸：
把绕点任意旋转，若
，
，请直接列式求出
面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
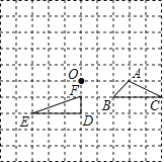
【题目】如图，在边长为1个单位长度的小正方形组成的网络中，给出了△ABC和△DEF（网点为网格线的交点）
（1）将△ABC向左平移两个单位长度，再向上平移三个单位长度，画出平移后的图形△A1B2C3；
（2）画出以点O为对称中心，与△DEF成中心对称的图形△D2E2F2；
（3）求∠C+∠E的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一些完全相同的小正方形搭成一个几何体，这个几何体从正面和左面看所得的平面图形均如图所示，小正方体的块数可能有（ ）
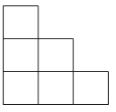
A. 7种 B. 8种 C. 9种 D. 10种
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数y=kx+b的图象经过点A（-2，6），且与x轴交于点B，与正比例函数y=3x的图象相交于点C，点C的横坐标是1．
（1）求此一次函数的解析式；
（2）请直接写出不等式（k-3）x+b＞0的解集；
（3）设一次函数y=kx+b的图象与y轴交于点M，点N在坐标轴上，当△CMN是直角三角形时，请直接写出所有符合条件的点N的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，由4个全等的正方形组成L形图案，请按下列要求画图：
(1)在图①中添加1个正方形，使它成轴对称图形（不能是中心对称图形）；
(2)在图②中添加1个正方形，使它成中心对称图形（不能是轴对称图形）；
(3)在图③中改变1个正方形的位置，从而得到一个新图形，使它既成中心对称图形，又成轴对称图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E、 F为AB上的一点,CF⊥AD于H，下列判断正确的有( )
A.AD是△ABE的角平分线B.BE是△ABD边AD上的中线
C.AH为△ABC的角平分线D.CH为△ACD边AD上的高
查看答案和解析>>
科目：初中数学 来源： 题型：
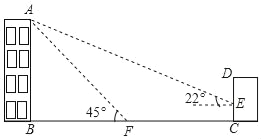
【题目】如图，小明想测量学校教学楼的高度，教学楼AB的后面有一建筑物CD，他测得当光线与地面成22°的夹角时，教学楼在建筑物的墙上留下高2米高的影子CE；而当光线与地面成45°的夹角时，教学楼顶A在地面上的影子F与墙角C有13米的距离（点B，F，C在同一条直线上），则AE之间的长为_____米．（结果精确到lm，参考数据：sin22°≈0.375，cos22°≈0.9375，tan22°≈0.4）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com