
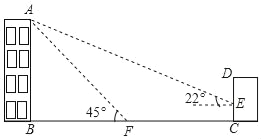
【题目】如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2米高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13米的距离(点B,F,C在同一条直线上),则AE之间的长为_____米.(结果精确到lm,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 为等边三角形,点
为等边三角形,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、点
、点![]() 重合).连接
重合).连接![]() ,以
,以![]() 为边向逆时针方向作等边
为边向逆时针方向作等边![]() ,连接
,连接![]() ,
,
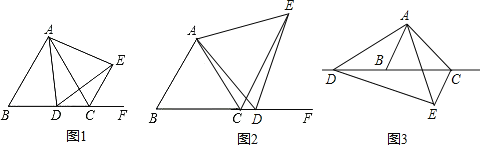
(1)如图1,当点![]() 在边
在边![]() 上时:
上时:
①求证:![]() ;
;
②判断![]() 之间的数量关系是 ;
之间的数量关系是 ;
(2)如图2,当点![]() 在边
在边![]() 的延长线上时,其他条件不变,判断
的延长线上时,其他条件不变,判断![]() 之间存在的数量关系,并写出证明过程;
之间存在的数量关系,并写出证明过程;
(3)如图3,当点![]() 在边
在边![]() 的反向延长线上时,其他条件不变,请直接写出
的反向延长线上时,其他条件不变,请直接写出![]() 之间存在的数量关系为 .
之间存在的数量关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
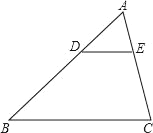
【题目】如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.
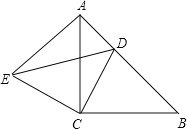
(1)求证:AE=BD;
(2)试探究线段AD、BD与CD之间的数量关系;
(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2![]() ,CD=
,CD=![]() ,求线段AB的长.
,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
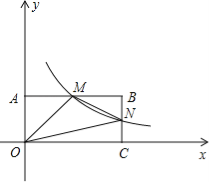
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
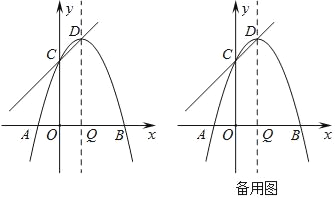
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A、B均在由面积为1的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是![]() 轴上使得∣PA—PB∣的值最大的点,Q是
轴上使得∣PA—PB∣的值最大的点,Q是![]() 轴上使得QA+QB的值最小的点,则OP·OQ=__________.
轴上使得QA+QB的值最小的点,则OP·OQ=__________.
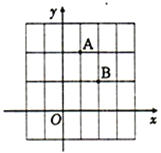
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:同学们在操场的一个圆形区域内玩投掷沙包的游戏,圆形区域由5个过同一点且半径不同的圆组成.经过多次实验,发现沙包如果都能落在区域内时,落在2、4两个阴影内的概率分别是0.36和0.21,设最大的圆的直径是5米,则1、3、5三个区域的面积和是_____.
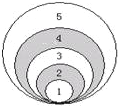
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com