
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
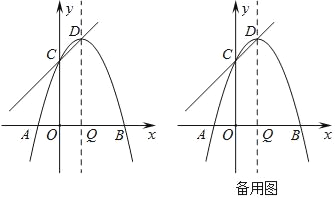
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)(1,﹣4+2![]() )或(1,﹣4﹣2
)或(1,﹣4﹣2![]() )(3)点M的坐标为(1,
)(3)点M的坐标为(1,![]() )或(1,1)
)或(1,1)
【解析】试题分析:![]()
![]() 求出
求出![]() 用待定系数法即可求出抛物线的解析式.
用待定系数法即可求出抛物线的解析式.
![]() 设直线CD切⊙P于点E.连结PE、PA,作
设直线CD切⊙P于点E.连结PE、PA,作![]() 点
点![]() .根据抛物线的解析式求出
.根据抛物线的解析式求出![]() 设
设![]()
![]() 设
设![]()
![]()
![]() 列出方程,求出
列出方程,求出![]() 的值.
的值.
![]() 分两种情况进行讨论即可.
分两种情况进行讨论即可.
试题解析:(1)![]()
∴![]()
代入![]() ,得
,得![]()
解得 ![]()
∴抛物线对应二次函数的表达式为:![]()
(2)如图,设直线CD切⊙P于点E.连结PE、PA,作![]() 点
点![]() .
.
![]() 由
由![]() 得对称轴为直线x=1,
得对称轴为直线x=1,
∴![]()
∴![]()
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴![]()
∴![]()
∴![]()
∴![]() 为等腰三角形.
为等腰三角形.
设![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
整理,得![]()
解得,![]()
∴点P的坐标为![]() 或
或![]()

(3)存在点M,使得![]() ∽
∽![]() .
.
如图,连结![]()
∵![]()
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]()
由(2)可知,![]()
∴![]()
∴![]() 分两种情况.
分两种情况.
当![]() 时,
时,
∴![]() ,解得
,解得![]() .
.
∴![]()
∴![]()
当![]() 时,
时,
∴![]() ,解得
,解得![]()
∴![]()
∴![]()
综上,点M的坐标为![]() 或
或![]()



科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
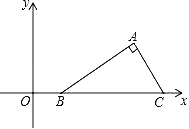
A. (﹣4,﹣2﹣![]() ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+![]() ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+![]() ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园手工制作活动中,甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同
(1)求甲、乙两人每小时各制作纸花多少朵?
(2)本次活动学校需要该种纸花不少于350朵,若由甲、乙两人共同制作,则至少需要几小时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
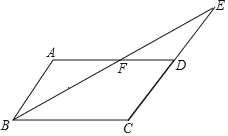
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a<0)的图象与x轴的两个交点A、B的横坐标分别为﹣3、1,与y轴交于点C,下面四个结论:①16a+4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣
,y2)是函数图象上的两点,则y1>y2;③c=﹣3a;④若△ABC是等腰三角形,则b=﹣![]() 或﹣
或﹣![]() .其中正确的有_____.(请将正确结论的序号全部填在横线上)
.其中正确的有_____.(请将正确结论的序号全部填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图顺次连接等腰梯形四边中点得到一个四边形,再顺次连接所得四边形四边的中点得到的图形是( )
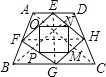
A. 等腰梯形B. 直角梯形C. 菱形D. 矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
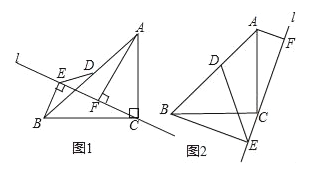
【题目】如图1,△ABC中,CA=CB,∠ACB=90°,直线l经过点C,AF⊥l于点F,BE⊥l于点E.
(1)求证:△ACF≌△CBE;
(2)将直线旋转到如图2所示位置,点D是AB的中点,连接DE.若AB=![]() ,∠CBE=30°,求DE的长.
,∠CBE=30°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
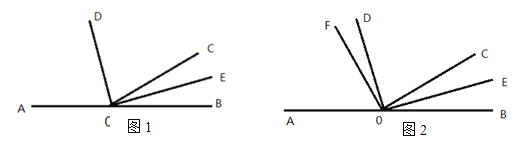
【题目】如图1,已知A、O、B三点在同一直线上,射线OD、OE分别平分∠AOC、∠BOC
(1)求∠DOE的度数;
(2)如图2,在∠AOD内引一条射线OF,使∠COF=![]() ,其他不变,设∠DOF=
,其他不变,设∠DOF=![]()
![]() )
)
①求∠AOF的度数(用含![]() 的代数式表示).
的代数式表示).
②若∠BOD是∠AOF的2倍,求∠DOF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com