
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).

【答案】①②③.
【解析】
①根据正方形的性质得到∠BAD=∠ADC=∠B=90°,根据旋转的性质得到∴∠NAD=∠BAM,∠AND=∠AMB,根据余角的性质得到∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,可知∠DAM=∠AND,②根据旋转的性质得到GN=ME,等量代换得到AB=ME=NG,根据全等三角形的判定定理得到△ABM≌△NGF;③由旋转的性质得到AM=AN,NF=MF,根据全等三角形的性质得到AM=NF,推出四边形AMFN是矩形,根据余角的想知道的∠NAM=90°,推出四边形AMFN是正方形,于是得到S四边形AMFN=AM2=a2+b2;
①∵四边形ABCD是正方形,
∴∠BAD=∠ADC=∠B=90°,
∴∠BAM+∠DAM=90°,
∵将△ABM绕点A旋转至△ADN,
∴∠NAD=∠BAM,∠AND=∠AMB,
∴∠DAM+∠NAD=∠NAD+∠AND=∠AND+∠NAD=90°,
∴∠DAM=∠AND,故①正确,
②∵将△MEF绕点F旋转至△NGF,
∴GN=ME,
∵AB=a,ME=a,
∴AB=ME=NG,
在△ABM与△NGF中,AB=NG=a,∠B=∠NGF=90°,GF=BM=b,
∴△ABM≌△NGF;故②正确;
③∵将△ABM绕点A旋转至△ADN,
∴AM=AN,
∵将△MEF绕点F旋转至△NGF,
∴NF=MF,
∵△ABM≌△NGF,
∴AM=NF,
∴四边形AMFN是矩形,
∵∠BAM=∠NAD,
∴∠BAM+DAM=∠NAD+∠DAN=90°,
∴∠NAM=90°,
∴四边形AMFN是正方形,
∵在Rt△ABM中,a2+b2=AM2,
∴S四边形AMFN=AM2=a2+b2;故③正确
故答案为:①②③.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
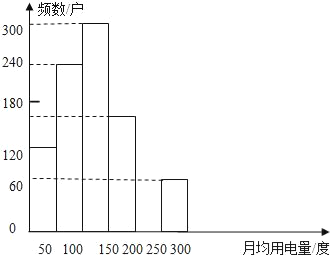
【题目】近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:
月均用电量a/度 | 频数/户 | 频率 |
0≤a<50 | 120 | 0.12 |
50≤a<100 | 240 | n |
100≤a<150 | 300 | 0.30 |
150≤a<200 | m | 0.16 |
200≤a<250 | 120 | 0.12 |
250≤a<300 | 60 | 0.06 |
合 计 | 1000 | 1 |
(1)频数分布表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
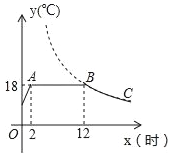
【题目】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线![]() 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=15时,大棚内的温度约为多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
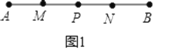
【题目】如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
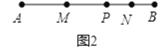
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于点A、B,与y轴交于点C,且OA=1,OB=3,顶点为D,对称轴交x轴于点Q.
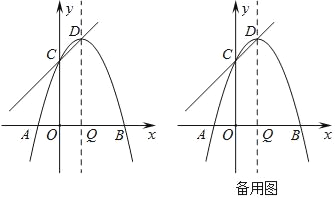
(1)求抛物线对应的二次函数的表达式;
(2)点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(3)在抛物线的对称轴上是否存在一点M,使得△DCM∽△BQC?如果存在,求出点M的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
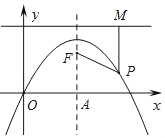
【题目】如图,抛物线y=﹣x2+2x的对称轴与x轴交于点A,点F在抛物线的对称轴上,且点F的纵坐标为![]() .过抛物线上一点P(m,n)向直线y=
.过抛物线上一点P(m,n)向直线y=![]() 作垂线,垂足为M,连结PF.
作垂线,垂足为M,连结PF.
(1)当m=2时,求证:PF=PM;
(2)当点P为抛物线上任意一点时,PF=PM是否还成立?若成立,请给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有A、B、C三地,C地位于A、B两地之间,甲车从A地沿这条公路匀速驶向C地,乙车从B地沿这条公路匀速驶向A地,在甲车出发至甲车到达C地的过程中,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.下列结论:①甲车出发2h时,两车相遇;②乙车出发1.5h时,两车相距170km;③乙车出发![]() h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).
h时,两车相遇;④甲车到达C地时,两车相距40km.其中正确的是______(填写所有正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】永辉超市销售茶壶、茶杯,茶壶每只定价20元,茶杯每只4元.今年“双十一”期间超市将开展促销活动,向顾客提供两种优惠方案:
方案一:每买一只茶壶就赠一只茶杯;
方案二:茶壶和茶杯都按定价的90%付款.
某顾客计划到该超市购买茶壶5只和茶杯![]() 只(茶杯数多于5只).
只(茶杯数多于5只).
(1)用含![]() 的代数式分别表示方案一与方案二各需付款多少元?
的代数式分别表示方案一与方案二各需付款多少元?
(2)当![]() 时,请通过计算说明该顾客选择上面的两种购买方案哪种更省钱?
时,请通过计算说明该顾客选择上面的两种购买方案哪种更省钱?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
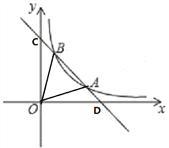
【题目】如图,一次函数y1=﹣2x+8的图象与反比例函数y2=![]() (x>0)的图象交于A(3,n),B(m,6)两点.
(x>0)的图象交于A(3,n),B(m,6)两点.
(1)求反比例函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当x>0时,y1>y2的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com