
����Ŀ�����Գ������۲�����豭�����ÿֻ����20Ԫ���豭ÿֻ4Ԫ��������˫ʮһ���ڼ䳬�н���չ���������˿��ṩ�����Żݷ���:
����һ��ÿ��һֻ�������һֻ�豭��
������������Ͳ豭�������۵�90%���
ij�˿ͼƻ����ó��й�����5ֻ�Ͳ豭![]() ֻ���豭������5ֻ��.
ֻ���豭������5ֻ��.
��1���ú�![]() �Ĵ���ʽ�ֱ��ʾ����һ�뷽�������踶�����Ԫ��
�Ĵ���ʽ�ֱ��ʾ����һ�뷽�������踶�����Ԫ��
��2����![]() ʱ����ͨ������˵���ù˿�ѡ����������ֹ������ָ�ʡǮ��
ʱ����ͨ������˵���ù˿�ѡ����������ֹ������ָ�ʡǮ��
��3����![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����
���𰸡�(1) ��1������һ�踶�4x��80��Ԫ���������踶�3.6x��90��Ԫ��(2)����һʡǮ��(3)��������
��������
(1)���������Żݷ����ֱ��г�����ʽ���ɣ�
(2)�ֱ����![]() ���м��㣬�ٱȽϼ��ɣ�
���м��㣬�ٱȽϼ��ɣ�
(3)�����ַ���������Ϲ��ɣ�
�⣺��1���˿Ͱ�����һ��������Ҫ����5��20��4��x5������4x��80��Ԫ��
�˿Ͱ���������������Ҫ����5��20��0.9��4��0.9x����3.6x��90��Ԫ��
��2����x��20Ԫʱ��
����һ�踶�4x��80��4��20��80��160��Ԫ����
�������踶�3.6x��90��3.6��20��90��162��Ԫ����
160��162��
��ѡ��һ�����ʡǮ��
��3���Ȱ�����һ����5�Ѳ��������5���豭������100Ԫ���ٰ�����������15���豭����15��4��0.9��54��Ԫ��������154Ԫ��
�˷����ȷ���һ��������ʡǮ��


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�BEƽ����ABC��CD���ӳ����ڵ�E����CF��BE��F��
(1)��֤��BF=EF��
(2)��AB=8��DE=4����ƽ���ı���ABCD���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���õ����������Σ���������ABCD�߳�Ϊa��С������CEFG�߳�Ϊb��a��b����M��BC����һ�����㣬����AM��MF��MF��CG�ڵ�P������ABM�Ƶ�A��ת����ADN������MEF�Ƶ�F��תǡ������NGF�����������������ۣ��١�AND=��MPC�� �ڡ�ABM�ա�NGF����S�ı���AMFN=a2+b2��
������ȷ�Ľ�����_____������д��ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����x�����������A��B�ĺ�����ֱ�Ϊ��3��1����y�ύ�ڵ�C�������ĸ����ۣ���16a+4b+c��0������P����5��y1����Q��![]() ��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��
��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��![]() ��
��![]() ��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
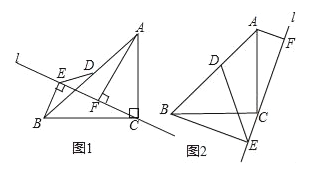
����Ŀ����ͼ1����ABC����CA=CB����ACB=90�㣬ֱ��l������C��AF��l�ڵ�F��BE��l�ڵ�E��
��1����֤����ACF�ա�CBE��
��2����ֱ����ת����ͼ2��ʾλ������D��AB���е�������DE����AB=![]() ����CBE=30�㣬��DE�ij���
����CBE=30�㣬��DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B��C��ֱ��Ϊ6cm�ġ�O�ϵĵ㣬��AB=3cm��AC=3![]() cm�����BAC�Ķ���Ϊ���� ����
cm�����BAC�Ķ���Ϊ���� ����
A. 15�� B. 75���15�� C. 105���15�� D. 75���105��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̻����Ӧ���⣺
��A�ص�B���������г�·�ߣ�
·��һ��ȫ��30ǧ�ף���·����̫�ã�
·�߶���ȫ��36ǧ�ף���·���ȽϺã�
һ���������·�߶���ƽ����������·��һ��ƽ�����ٵ�1.8������·�߶����õ�ʱ�����·��һ���õ�ʱ����20���ӣ���ô��·�߶���ƽ��������ÿСʱ����ǧ�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס������������IJ������װ��3����С��������ȫ��ͬ��С�����м״��е�С���Ϸֱ��������0��1��2���Ҵ��е�С���Ϸֱ�������֩�1����2��0���ִӼ״�����������һ��С������е�����Ϊx���ٴ��Ҵ�����������һ��С������е�����Ϊy���Դ�ȷ����M�����꣨x��y����
��1�������û���״ͼ���б��ķ�����д����M���п��ܵ����ꣻ
��2�����M��x��y���ں���y=��![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC����C=90�㣬CA=CB=4![]() cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���
cm����PΪAB���ϵ�һ�����㣬��E��CA�ߵ��е�, ����PE����A��P�����ľ���Ϊxcm��P��E�����ľ���Ϊy cm.С������ѧϰ�����ľ��飬�Ժ���![]() ���Ա���
���Ա���![]() �ı仯���仯�Ĺ��ɽ�����̽����
�ı仯���仯�Ĺ��ɽ�����̽����
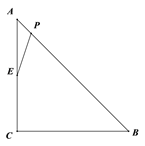
������С����̽�����̣��벹��������
��1��ͨ��ȡ�㡢��ͼ���������õ���![]() ��
��![]() �ļ���ֵ�����±���
�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
��˵������ȫ����ʱ�����ֵ����һλС����
��2������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��

��3����ϻ����ĺ���ͼ������⣺
��д���ú�����һ�����ʣ� ��
�ڵ�![]() ʱ��
ʱ��![]() �ij���ԼΪ cm.
�ij���ԼΪ cm.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com