
【题目】列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,
一般情况下走路线二的平均车速是走路线一的平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.那么走路线二的平均车速是每小时多少千米?
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】(11·漳州)(满分8分)漳州市某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:

(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有_ ▲ 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
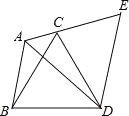
【题目】如图,已知△ABC,以BC为边向外作△BCD并连接AD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,且点A,C,E在一条直线上,若AB=3,AC=2,求∠BAD的度数与AD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°.若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( ) 
A.1元
B.2元
C.3元
D.4元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE. 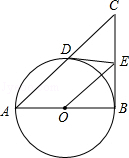
(1)试判断OE与AC的关系,并说明理由;
(2)填空: ①当∠BAC=时,四边形ODEB是正方形.
②当∠BAC=30°时, ![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com