
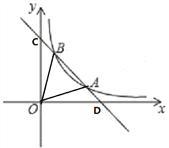
【题目】如图,一次函数y1=﹣2x+8的图象与反比例函数y2=![]() (x>0)的图象交于A(3,n),B(m,6)两点.
(x>0)的图象交于A(3,n),B(m,6)两点.
(1)求反比例函数的解析式;
(2)求△OAB的面积;
(3)根据图象直接写出当x>0时,y1>y2的自变量x的取值范围.
【答案】(1)反比例函数的解析式为![]() ;(2)8;(3) 1<x<3
;(2)8;(3) 1<x<3
【解析】试题分析:(1)把![]() 两点分别代入
两点分别代入![]() 可求出
可求出![]() 的值,确定
的值,确定![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,然后利用待定系数法求反比例函数的解析式;
,然后利用待定系数法求反比例函数的解析式;
(2)求得直线与![]() 轴的交点坐标,根据三角形面积公式即可求得.
轴的交点坐标,根据三角形面积公式即可求得.
(3)观察函数图象得到当![]() 时,一次函数图象在反比例函数的图象上方.
时,一次函数图象在反比例函数的图象上方.
试题解析:
(1)把A(3,n),B(m,6)两点分别代入y=2x+8得6=m+8,n=2×3+8,解得m=1,n=2,
∴A点坐标为(3,2),B点坐标为(1,6),
把A(3,2)代入![]() ,求得k=1×6=6,
,求得k=1×6=6,
∴反比例函数解析式为![]()
(2)![]() 时x的取值范围是
时x的取值范围是![]()
(3)由直线y=2x+8可知与x轴的交点为D (4,0),
∴![]()


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,
一般情况下走路线二的平均车速是走路线一的平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.那么走路线二的平均车速是每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
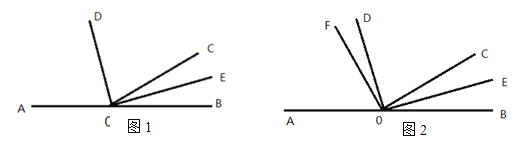
【题目】如图1,已知A、O、B三点在同一直线上,射线OD、OE分别平分∠AOC、∠BOC
(1)求∠DOE的度数;
(2)如图2,在∠AOD内引一条射线OF,使∠COF=![]() ,其他不变,设∠DOF=
,其他不变,设∠DOF=![]()
![]() )
)
①求∠AOF的度数(用含![]() 的代数式表示).
的代数式表示).
②若∠BOD是∠AOF的2倍,求∠DOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段![]() 上.点P从点C出发向点
上.点P从点C出发向点![]() 运动,速度为2cm/s;同时,点Q也从点C以4cm/s速度出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,.最终,点Q比点P早1s到达B处.设点P运动的时间为t.
运动,速度为2cm/s;同时,点Q也从点C以4cm/s速度出发用1s到达A处,并在A处停留2s,然后按原速度向点B运动,.最终,点Q比点P早1s到达B处.设点P运动的时间为t.
(1)线段AC的长为 cm;当t=3s时,P,Q两点之间的距离为 cm;
(2)求线段BC的长;
(3)从P,Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P,Q两点相距1cm?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.请根据图中的信息,解答下列问题:

(1)在这次调查中,一共抽取了________名学生,a=________%;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为________度;
(4)若该校共有2 000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
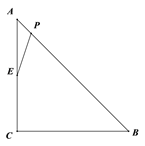
【题目】如图,Rt△ABC,∠C=90°,CA=CB=4![]() cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当![]() 时,
时,![]() 的长度约为 cm.
的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com