
【题目】近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:
月均用电量a/度 | 频数/户 | 频率 |
0≤a<50 | 120 | 0.12 |
50≤a<100 | 240 | n |
100≤a<150 | 300 | 0.30 |
150≤a<200 | m | 0.16 |
200≤a<250 | 120 | 0.12 |
250≤a<300 | 60 | 0.06 |
合 计 | 1000 | 1 |
(1)频数分布表中的m=_____,n=_____;
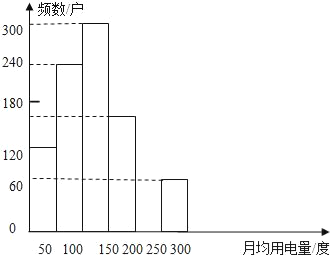
(2)补全频数分布直方图;
(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】某市为了美化环境,计划在一定的时间内完成绿化面积![]() 万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加
万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加![]() ,而且要提前
,而且要提前![]() 年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多
年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多![]() 万亩,求原计划平均每年的绿化面积.
万亩,求原计划平均每年的绿化面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
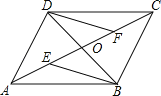
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=![]() AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
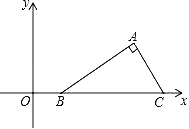
【题目】如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
A. (﹣4,﹣2﹣![]() ) B. (﹣4,﹣2+
) B. (﹣4,﹣2+![]() ) C. (﹣2,﹣2+
) C. (﹣2,﹣2+![]() ) D. (﹣2,﹣2﹣
) D. (﹣2,﹣2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,每套西装的定价为300元,每条领带的定价为50元,厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的![]() 付款.
付款.
现某客户要到该服装厂购买西装20套,领带![]() 条(
条(![]() )
)
(1)若该客户按方案①购买,则需付款____________元(用含![]() 的代数式表示);
的代数式表示);
若该客户按方案②购买,则需付款____________元(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,则通过计算说明此时按哪种方案购买较为合算.
,则通过计算说明此时按哪种方案购买较为合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年夏天,浙江省遭遇了持续高温,导致茶叶大幅减产,因而造成价格上涨,每千克的价格是去年同期的2倍.茶农陈某今年第三季度的茶叶产量为120千克,比去年同期减少了40%,但销售收入却比去年同期增加了2000元.
(1)茶农陈某去年第三季度的茶叶产量为______千克.
(2)根据题意,甲、乙两名同学分别列出尚不完整的方程如下:
甲:( )×2x-( )·x=2000
乙:![]()
根据甲、乙两名同学所列的方程,请你分别指出未知数x表示的意义,然后再写出甲、乙两名同学所列的方程.
甲:x表示_______________________,
乙:x表示__________________.
甲同学所列的方程是:_____________,
乙同学所列的方程是:____________.
(3)陈某今年第三季度茶叶销售收入为多少元?(写出完整的解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BE平分∠ABC交CD的延长线于点E,作CF⊥BE于F.
(1)求证:BF=EF;
(2)若AB=8,DE=4,求平行四边形ABCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com