
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=![]() AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
AC,则四边形ABCD是什么特殊四边形?请证明你的结论.
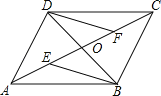
【答案】矩形.
【解析】试题分析:(1)由DF与BE平行,得到两对内错角相等,再由O为AC的中点,得到OA=OC,又AE=CF,得到OE=OF,利用AAS即可得证;
(2)若OD=![]() AC,则四边形ABCD为矩形,理由为:由OD=
AC,则四边形ABCD为矩形,理由为:由OD=![]() AC,得到OB=
AC,得到OB=![]() AC,即OD=OA=OC=OB,利用对角线互相平分且相等的四边形为矩形即可得证.
AC,即OD=OA=OC=OB,利用对角线互相平分且相等的四边形为矩形即可得证.
试题解析:(1)∵DF∥BE,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,
∴OA=OC,
∵AE=CF,
∴OA-AE=OC-CF,
即OE=OF,
在△BOE和△DOF中,
 ,
,
∴△BOE≌△DOF(AAS);
(2)若OD=![]() AC,则四边形ABCD是矩形,理由为:
AC,则四边形ABCD是矩形,理由为:
证明:∵△BOE≌△DOF,
∴OB=OD,
∵OD=![]() AC,
AC,
∴OA=OB=OC=OD,且BD=AC,
∴四边形ABCD为矩形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点![]() 、
、![]() 、
、![]() 是数轴上三点,点
是数轴上三点,点![]() 表示的数为
表示的数为![]() ,
, ![]() ,
, ![]() .
.
(![]() )写出数轴上点
)写出数轴上点![]() 、
、![]() 表示的数:__________,__________.
表示的数:__________,__________.
(![]() )动点
)动点![]() ,
, ![]() 同时从
同时从![]() ,
, ![]() 出发,点
出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴向右匀速运动,点
个单位长度的速度沿数轴向右匀速运动,点![]() 以
以![]() 个单位长度的速度沿数向左匀速运动,设运动时间为
个单位长度的速度沿数向左匀速运动,设运动时间为![]() 秒.
秒.
①求数轴上点![]() ,
, ![]() 表示的数(用含
表示的数(用含![]() 的式子表示);
的式子表示);
②![]() 为何值时,点
为何值时,点![]() ,
, ![]() 相距
相距![]() 个单位长度.
个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为4kg(在弹性限度内)时,弹簧的总长L(cm)是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级A班有50人,某次活动中分为三组,第一组有(3a+4b+2)人,第二组比第一组的一半多6人.
(1)求第三组的人数;(用含a,b的整式表示)
(2)试判断当a=1,b=2时,是否满足题意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 过点
过点![]() ,直线
,直线![]() :
:![]() 与直线
与直线![]() 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
① 当b=4时,直接写出△OBC内的整点个数;
②若△OBC内的整点个数恰有4个,结合图象,求b的取值范围.
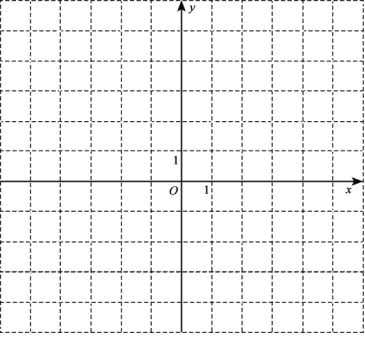
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:
月均用电量a/度 | 频数/户 | 频率 |
0≤a<50 | 120 | 0.12 |
50≤a<100 | 240 | n |
100≤a<150 | 300 | 0.30 |
150≤a<200 | m | 0.16 |
200≤a<250 | 120 | 0.12 |
250≤a<300 | 60 | 0.06 |
合 计 | 1000 | 1 |
(1)频数分布表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.
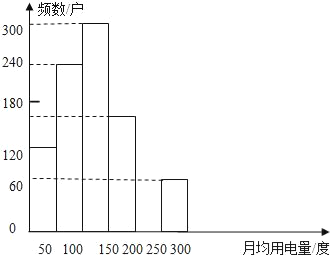
查看答案和解析>>
科目:初中数学 来源: 题型:
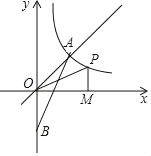
【题目】如图,点P是反比例函数y=![]() (k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,若△POM的面积为2.
(k>0)图象在第一象限上的一个动点,过P作x轴的垂线,垂足为M,若△POM的面积为2.
(1)求反比例函数的解析式;
(2)若点B坐标为(0,﹣2),点A为直线y=x与反比例函数y=![]() (k>0)图象在第一象限上的交点,连接AB,过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
(k>0)图象在第一象限上的交点,连接AB,过A作AC⊥y轴于点C,若△ABC与△POM相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
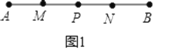
【题目】如图,点P是线段AB上的一点,点M、N分别是线段AP、PB的中点.
(1)如图1,若点P是线段AB的中点,且MP=4cm,求线段AB的长;
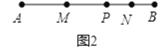
(2)如图2,若点P是线段AB上的任一点,且AB=12cm,求线段MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com