练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某市为了美化环境，计划在一定的时间内完成绿化面积万亩的任务，后来市政府调整了原定计划，不但绿化面积要在原计划的基础上增加，而且要提前年完成任务，经测算要完成新的计划，平均每年的绿化面积必须比原计划多万亩，求原计划平均每年的绿化面积．

    【答案】原计划平均每年完成绿化面积万亩.

    【解析】

    本题的相等关系是：原计划完成绿化时间实际完成绿化实际＝1．设原计划平均每年完成绿化面积x万亩，则原计划完成绿化完成时间年，实际完成绿化完成时间：年，列出分式方程求解

    解：设原计划平均每年完成绿化面积万亩.

    根据题意可列方程：

    去分母整理得：

    解得：，

    经检验：，都是原分式方程的根，因为绿化面积不能为负，所以取．

    答：原计划平均每年完成绿化面积万亩.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：如图①，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点，点P在该抛物线上(P点与A、B两点不重合)．如果△ABP的三边满足AP2＋BP2＝AB2，则称点P为抛物线y＝ax2＋bx＋c(a≠0)的勾股点．

    (1)直接写出抛物线y＝－x2＋1的勾股点的坐标．

    (2)如图②，已知抛物线y＝ax2＋bx(a≠0)与x轴交于A，B两点，点P(1， )是抛物线的勾股点，求抛物线的函数表达式．

    (3)在(2)的条件下，点Q在抛物线上，求满足条件S△ABQ＝S△ABP的Q点(异于点P)的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

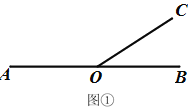
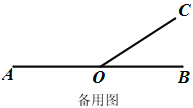
    【题目】已知：如图1，点O是直线AB上一点，过点O作射线OC.

    (1)若∠AOC=140°，则∠BOC=________°.

    (2)在图1中分别画∠AOC的角平分线OE和∠BOC的角平分线OF，那么,OE和OF有什么位置关系，请说明理由.

    (3)若∠BOC=30°，射线OD从OB出发，绕点O以每秒10°角的速度逆时针旋转.当射线OD与射线OA重合时，射线OC以每秒30°角的速度绕点O逆时针旋转，射线OD按原来的速度和方向继续旋转，当射线OC或射线OD中有一条射线与射线OB重合时，两条射线都停止.设射线OD旋转的时间为t秒，在旋转的过程中，是否存在某个时刻，使得射线OB、OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在，直接写出所有满足条件的t的值，若不存在，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点、、是数轴上三点，点表示的数为， ， ．

    （）写出数轴上点、表示的数：__________，__________．

    （）动点， 同时从， 出发，点以每秒个单位长度的速度沿数轴向右匀速运动，点以个单位长度的速度沿数向左匀速运动，设运动时间为秒．

    ①求数轴上点， 表示的数（用含的式子表示）；

    ②为何值时，点， 相距个单位长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列方程没有实数根的是（　　）

    A. x3+2＝0B. x2+2x+2＝0

    C. ＝x﹣1D. ＝0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中假命题是（ ）

    A.在同一平面内，有三条直线、、，如果，，则

    B.当被开方数扩大到100倍时，算术平方根的结果扩大到10倍

    C.在同一平面内，有三条直线、、，如果，，则

    D.直线外一点到这条直线的垂线段的长度，叫做点到直线的距离

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示的正方形网格中，每个小正方形的边长均为1个单位长度，三角形的三个顶点都在格点上.

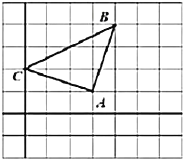
    （1）请你以为原点，建立平面直角坐标系，并写出、两点的坐标.

    （2）若三角形内部有一点，经过平移后的对应点的坐标为，且、、的对应点分别为、、，请说明三角形是如何由三角形平移得到（沿网格线平移），并画出三角形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，的顶点坐标分别为，，.

    （1）求的面积.

    （2）若交轴于点，请求出点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

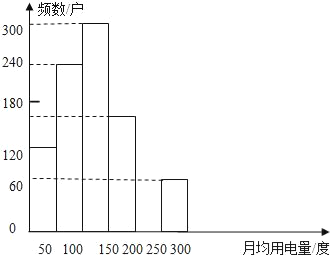
    【题目】近期，中宣部、国家发改委发出开展节俭养德全民节约行动的通知，在全社会营造厉行节约、拒绝浪费的浓厚氛围，我市某中学为了解该校学生家庭月均用电量情况，给学生布置了收集自己家中月均用电量数据的课外作业，学校随机抽取了1000名学生家庭月均用电量的数据，并将调查数据整理如下：

    月均用电量a/度

    频数/户

    频率

    0≤a＜50

    120

    0.12

    50≤a＜100

    240

    n

    100≤a＜150

    300

    0.30

    150≤a＜200

    m

    0.16

    200≤a＜250

    120

    0.12

    250≤a＜300

    60

    0.06

    合　　计

    1000

    1

    （1）频数分布表中的m=_____，n=_____；

    （2）补全频数分布直方图；

    （3）被调查的1000名学生家庭月均用电量的众数落在哪一个范围？

    （4）求月均用电量小于150度的家庭数占被调查家庭总数的百分比．

    查看答案和解析>>

    同步练习册答案