
����Ŀ�����壺��ͼ�٣�������y��ax2��bx��c(a��0)��x�ύ��A��B���㣬��P�ڸ���������(P����A��B���㲻�غ�)�������ABP����������AP2��BP2��AB2����Ƶ�PΪ������y��ax2��bx��c(a��0)�Ĺ��ɵ㣮
(1)ֱ��д��������y����x2��1�Ĺ��ɵ�����꣮
(2)��ͼ�ڣ���֪������y��ax2��bx(a��0)��x�ύ��A��B���㣬��P(1�� ![]() )�������ߵĹ��ɵ㣬�������ߵĺ�������ʽ��
)�������ߵĹ��ɵ㣬�������ߵĺ�������ʽ��
(3)��(2)�������£���Q���������ϣ�����������S��ABQ��S��ABP��Q��(���ڵ�P)�����꣮

���𰸡�(1)(0��1)(2) y��-![]() x(x-4)��-
x(x-4)��-![]() x2��
x2��![]() x(3)���������ĵ�Q��3�����ֱ�Ϊ(3��
x(3)���������ĵ�Q��3�����ֱ�Ϊ(3�� ![]() )��(2��
)��(2��![]() ����
���� ![]() )��(2��
)��(2��![]() ����
���� ![]() )��
)��
���������������:(1)���������߹��ɵ�Ķ���������,(2)��PG��x��,�ɵ�P���������:AG=1,PG=![]() ,�����Ǻ����ɵ�:
,�����Ǻ����ɵ�: ![]() ,��֪��PAG=60���Ӷ����AB=4,��B(4,0),����ϵ����������,(3)��
,��֪��PAG=60���Ӷ����AB=4,��B(4,0),����ϵ����������,(3)��![]() ������������ͬ��,��֪��Q��x��ľ���Ϊ
������������ͬ��,��֪��Q��x��ľ���Ϊ![]() ,�������.
,�������.
(1)������y����x2��1�Ĺ��ɵ������Ϊ(0��1)��
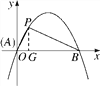
(2)��ͼ����PG��x���ڵ�G.�ߵ�P������Ϊ(1��![]() )����AG��1��PG��
)����AG��1��PG��![]() ����PA��
����PA��![]() ��
��![]() ��2.��tan��PAB��
��2.��tan��PAB��![]() ��
��![]() �����PAG��60��.��Rt��PAB��AB��
�����PAG��60��.��Rt��PAB��AB��![]() ��
��![]() ��4�����B������Ϊ(4��0)��
��4�����B������Ϊ(4��0)��
��y��ax(x��4)������P(1��![]() )�����a����
)�����a����![]() ����y����
����y����![]() x(x��4)����
x(x��4)����![]() x2��
x2��![]() x.
x.
(3)�ٵ���Q��x���Ϸ�ʱ����S��ABQ��S��ABP֪��Q��������Ϊ![]() �����У�
������![]() x2��
x2��![]() x��
x��![]() �����x1��3��x2��1(���������⣬��ȥ)�����Q������Ϊ(3��
�����x1��3��x2��1(���������⣬��ȥ)�����Q������Ϊ(3��![]() )��
)��
�ڵ���Q��x���·�ʱ����S��ABQ��S��ABP֪��Q��������Ϊ��![]() �����У�
������![]() x2��
x2��![]() x����
x����![]() �����x1��2��
�����x1��2��![]() ��x2��2��
��x2��2��![]() �����Q������Ϊ(2��
�����Q������Ϊ(2��![]() ����
����![]() )��(2��
)��(2��![]() ����
����![]() )��
)��
�������������������ĵ�Q��3�����ֱ�Ϊ(3��![]() )��(2��
)��(2��![]() ����
����![]() )��(2��
)��(2��![]() ����
����![]() )��
)��


 ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.a5+a5=a10
B.a7��a=a6
C.a3a2=a6
D.����a3��2=��a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������a1��a2��a3��a4��ƽ������2017������һ������a1+3��a2��2��a3��2��a4+5��ƽ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̨Ԥ�����������콵ˮ������85%�����Դ���Ϣ������˵����ȷ���ǣ� ��
A���������콫��85%�ĵ�����ˮ B���������콫��85%��ʱ�併ˮ
C�����콵ˮ�Ŀ����ԱȽϴ� D������϶�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺ ij��߳�����һ����ߣ����տ��ƹ̶��ɱ����۴�����ԭ��ʹ����������ܹ���ʱ�۳������г����飺ÿ����߰�480Ԫ����ʱ��ÿ�������160���������۵���ÿ����1Ԫ��ÿ��ɶ��۳�2������֪ÿ����ߵĹ̶��ɱ�Ϊ360Ԫ����������ߵ����۵���Ϊ����Ԫʱ������ÿ��ɻ�����20000Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1���������߾���A��1��0����C��0��3�����㣬��x�ύ�ڵ�B��
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2���������ߵĶԳ���x=��1����һ��M��ʹ��M����A�ľ����뵽��C�ľ���֮����С�������M�����ꣻ
��3�����PΪ�����ߵĶԳ���x=��1�ϵ�һ�����㣬��ʹ��BPCΪֱ�������εĵ�P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2��3x+m=0��һ������2����������һ������ �� m��ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������¼�����ȷ���¼����ǣ�������
A. �����н�ͨ�źŵƵ�·�ڣ������̵�
B. ��һ��ֻװ�к���Ĵ���������һ������
C. ���ӻ������ڲ��Ŷ���˹���籭
D. һ�����ľ���ֵΪ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com