
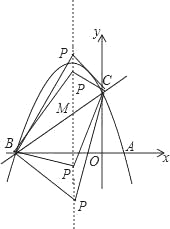
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.

【答案】(1)![]() ,
,![]() ;(2)M(-1,2);(3)P的坐标为(-1,-2)或(-1,4) 或(-1,
;(2)M(-1,2);(3)P的坐标为(-1,-2)或(-1,4) 或(-1,![]() ) 或(-1,
) 或(-1,![]() ).
).
【解析】试题分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
试题解析:(1)依题意得: 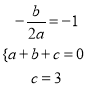 ,
,
解之得: 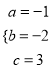
∴抛物线解析式为y=-x2-2x+3
∵对称轴为x=-1,且抛物线经过A(1,0),
∴把B(-3,0)、C(0,3)分别代入直线y=mx+n,
得![]() ,
,
解之得: ![]() ,
,
∴直线y=mx+n的解析式为y=x+3;
(2)设直线BC与对称轴x=-1的交点为M,则此时MA+MC的值最小.
把x=-1代入直线y=x+3得,y=2,
∴M(-1,2),
即当点M到点A的距离与到点C的距离之和最小时M的坐标为(-1,2);
(3)设P(-1,t),
又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,
PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2
即:18+4+t2=t2-6t+10解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2
即:18+t2-6t+10=4+t2解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2
即:4+t2+t2-6t+10=18解之得:t1=![]() ,t2=
,t2=![]() ;
;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1, ![]() ) 或(-1,
) 或(-1, ![]() ).
).


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】为了解某市5万名初中毕业生的中考数学成绩,从中抽取500名学生的中考数学成绩进行统计分析,那么样本是( )
A. 被抽取500名学生的中考数学成绩B. 5万名初中毕业生
C. 某市5万名初中毕业生的中考数学成绩D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图①,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(P点与A、B两点不重合).如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
(1)直接写出抛物线y=-x2+1的勾股点的坐标.
(2)如图②,已知抛物线y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1, ![]() )是抛物线的勾股点,求抛物线的函数表达式.
)是抛物线的勾股点,求抛物线的函数表达式.
(3)在(2)的条件下,点Q在抛物线上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2-3x+![]() 与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
与x轴相交于A、B两点,与y轴相交于点C,点D是直线BC下方抛物线上一点,过点D作y轴的平行线,与直线BC相交于点E.
(1)求直线BC的解析式;
(2)当线段DE的长度最大时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报纸上刊登了一则新闻,“某种品牌的节能灯的合格率为95%”,请据此回答下列问题:
(1)这则新闻是否说明市面上所有这种品牌的节能灯恰有5%为不合格?
(2)你认为这则消息来源于普查,还是抽样调查?为什么?
(3)如果已知在这次检查中合格产品有76个,则共有多少个节能灯接受检查?
(4)如果此次检查了两种产品,数据如下表所示,有人由此认为“A品牌的不合格率比B品牌低,更让人放心”.你同意这种说法吗?为什么?
品牌 | A品牌 | B品牌 |
被检测数 | 70 | 10 |
不合格数 | 3 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com