
【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,三角形![]() 的三个顶点都在格点上.
的三个顶点都在格点上.
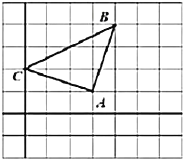
(1)请你以![]() 为原点
为原点![]() ,建立平面直角坐标系,并写出
,建立平面直角坐标系,并写出![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)若三角形![]() 内部有一点
内部有一点![]() ,经过平移后的对应点
,经过平移后的对应点![]() 的坐标为
的坐标为![]() ,且
,且![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() ,请说明三角形
,请说明三角形![]() 是如何由三角形
是如何由三角形![]() 平移得到(沿网格线平移),并画出三角形
平移得到(沿网格线平移),并画出三角形![]() .
.
【答案】(1)图见解析;点B的坐标为(1,3),点C的坐标为(﹣3,1);(2)先向右平移1个单位,然后再向下平移2个单位;图见解析.
【解析】
(1)根据题意,建立平面直角坐标系,然后写出B、C的坐标即可;
(2)根据P、Q两点坐标即可判断出点P到点Q的平移规律,从而得出:三角形ABC到三角形DEF的平移规律,根据平移规律画图即可.
解:(1)根据题意以![]() 为原点
为原点![]() ,建立平面直角坐标系,如下图所示,由图可知:点B的坐标为(1,3),点C的坐标为(﹣3,1);
,建立平面直角坐标系,如下图所示,由图可知:点B的坐标为(1,3),点C的坐标为(﹣3,1);
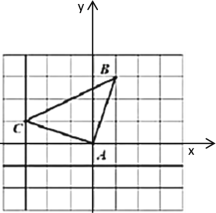
(2)∵点![]() ,经过平移后的对应点
,经过平移后的对应点![]() 的坐标为
的坐标为![]()
∴点P到点Q的平移规律是:先向右平移1个单位,然后再向下平移2个单位
∴三角形ABC到三角形DEF的平移规律是:先向右平移1个单位,然后再向下平移2个单位
如下图所示:三角形DEF即为所求.



科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析表达式为y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2,交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+n(m<0)的顶点为A,与x轴交于B,C两点(点B在点C左侧),与y轴正半轴交于点D,连接AD并延长交x轴于E,连AC、DC.S△DEC:S△AEC=3:4.
(1)求点E的坐标;
(2)△AEC能否为直角三角形?若能,求出此时抛物线的函数表达式;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了美化环境,计划在一定的时间内完成绿化面积![]() 万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加
万亩的任务,后来市政府调整了原定计划,不但绿化面积要在原计划的基础上增加![]() ,而且要提前
,而且要提前![]() 年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多
年完成任务,经测算要完成新的计划,平均每年的绿化面积必须比原计划多![]() 万亩,求原计划平均每年的绿化面积.
万亩,求原计划平均每年的绿化面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次中学生田径运动会上,参加男子跳高的20名运动员成绩如下所示:
成绩(单位:米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 4 | 5 | 2 | 1 | 1 |
则下列叙述正确的是( )
A. 这些运动员成绩的中位数是1.70
B. 这些运动员成绩的众数是5
C. 这些运动员的平均成绩是1.71875
D. 这些运动员成绩的中位数是1.726
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选出两个作为补充条件,使平行四边形ABCD成为正方形(如图所示).现有下列四种选法,你认为其中错误的是( )

A. ①②B. ②④C. ①③D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年夏天,浙江省遭遇了持续高温,导致茶叶大幅减产,因而造成价格上涨,每千克的价格是去年同期的2倍.茶农陈某今年第三季度的茶叶产量为120千克,比去年同期减少了40%,但销售收入却比去年同期增加了2000元.
(1)茶农陈某去年第三季度的茶叶产量为______千克.
(2)根据题意,甲、乙两名同学分别列出尚不完整的方程如下:
甲:( )×2x-( )·x=2000
乙:![]()
根据甲、乙两名同学所列的方程,请你分别指出未知数x表示的意义,然后再写出甲、乙两名同学所列的方程.
甲:x表示_______________________,
乙:x表示__________________.
甲同学所列的方程是:_____________,
乙同学所列的方程是:____________.
(3)陈某今年第三季度茶叶销售收入为多少元?(写出完整的解答过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com