
【题目】小明在学习了正方形之后,给同桌小文出了道题.从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中选出两个作为补充条件,使平行四边形ABCD成为正方形(如图所示).现有下列四种选法,你认为其中错误的是( )

A. ①②B. ②④C. ①③D. ②③
【答案】D
【解析】
利用矩形、菱形、正方形之间的关系与区别,结合正方形的判定方法分别判断得出即可.
A、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当②∠ABC=90°时,菱形ABCD是正方形,故此选项正确,不合题意;
B、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当④AC⊥BD时,矩形ABCD是正方形,故此选项正确,不合题意.
C、∵四边形ABCD是平行四边形,
当①AB=BC时,平行四边形ABCD是菱形,
当③AC=BD时,菱形ABCD是正方形,故此选项正确,不合题意;
D、∵四边形ABCD是平行四边形,
∴当②∠ABC=90°时,平行四边形ABCD是矩形,
当AC=BD时,这是矩形的性质,无法得出四边形ABCD是正方形,故此选项错误,符合题意.
故选D.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳绳 | 25 | a |
实心球 | 20 |
|
50m | b | 0.4 |
拔河 | 0.15 |
(1)直接写出a= ,b= ;
(2)将图中的扇形统计图补充完整(注明项目、百分比);
(3)若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,三角形![]() 的三个顶点都在格点上.
的三个顶点都在格点上.
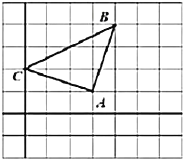
(1)请你以![]() 为原点
为原点![]() ,建立平面直角坐标系,并写出
,建立平面直角坐标系,并写出![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)若三角形![]() 内部有一点
内部有一点![]() ,经过平移后的对应点
,经过平移后的对应点![]() 的坐标为
的坐标为![]() ,且
,且![]() 、
、![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() 、
、![]() ,请说明三角形
,请说明三角形![]() 是如何由三角形
是如何由三角形![]() 平移得到(沿网格线平移),并画出三角形
平移得到(沿网格线平移),并画出三角形![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级A班有50人,某次活动中分为三组,第一组有(3a+4b+2)人,第二组比第一组的一半多6人.
(1)求第三组的人数;(用含a,b的整式表示)
(2)试判断当a=1,b=2时,是否满足题意.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,甲、乙两个小组进行定点投篮对抗赛,每组10人,每人投10次.下表是甲组成绩统计表:
投进个数 | 10个 | 8个 | 6个 | 4个 |
人数 | 1个 | 5人 | 2人 | 2人 |
(1)请计算甲组平均每人投进个数;
(2)经统计,两组平均每人投进个数相同且乙组成的方差为3.2.若从成绩稳定性角度看,哪一组表现更好?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com