
����Ŀ����ͼ1��ABCDΪ�����Σ��������εı�CB�Ƶ�C˳ʱ����ת��CE������BCE=��������BE��DE������C��CF��DE��F����ֱ��BE��H��
��1������=60��ʱ����ͼ1������BHC= ��
��2����45�㣼����90������ͼ2���߶�BH��EH��CH֮�����һ���ض���������ϵ������ͨ��̽����д�������ϵʽ�� ������֤������
��3����90�㣼����180���������������䣨��ͼ3������2���еĹ�ϵʽ�Ƿ�������������˵�����ɣ�����������д������Ϊ�����Ľ��ۣ�����Ҫ֤����

���𰸡���1��45�㣻��2��BH+EH=![]() CH����3����������BH��EH=
CH����3����������BH��EH=![]() CH��
CH��
�������������������1����CG��BH��G���������ε����ʺ���ת�����ʵó���BCE=��=60�㣬CB=CD=CE���ɵ��������ε����ʵó���BCG=��ECG=![]() ��BCE=30�㣬��ECF=��DCF=
��BCE=30�㣬��ECF=��DCF=![]() ��DCE�������GCH=
��DCE�������GCH=![]() ����BCE+��DCE��=45�㼴�ɣ�
����BCE+��DCE��=45�㼴�ɣ�
��2����CG��BH��G��ͬ��1���ã���BHC=45�㣬��CGH�ǵ���ֱ�������Σ��ɵ���ֱ�������ε����ʺ��ɶ����ó�CH=![]() GH���ɵ��������ε����ʵó�BG=EG=
GH���ɵ��������ε����ʵó�BG=EG=![]() BE�����ɵó����ۣ�
BE�����ɵó����ۣ�
��3����CG��BH��G��ͬ��2���ã���BHC=45�㣬��CGH�ǵ���ֱ�������Σ�CH=![]() GH��BG=EG=
GH��BG=EG=![]() BE�����ɵó����ۣ�
BE�����ɵó����ۣ�
����������⣺��1����CG��BH��G����ͼ1��ʾ��
���ı���ABCD�������Σ���CB=CD����BCD=90�㣬����ת�����ʵã�CE=CB����BCE=��=60�㣬��CD=CE����BCG=��ECG=![]() ��BCE=30�㣮��CF��DE�����ECF=��DCF=
��BCE=30�㣮��CF��DE�����ECF=��DCF=![]() ��DCE�����GCH=
��DCE�����GCH=![]() ����BCE+��DCE��=
����BCE+��DCE��=![]() ��90��=45�㣻�ʴ�Ϊ��45�㣻
��90��=45�㣻�ʴ�Ϊ��45�㣻
��2��BH+EH=![]() CH���������£�
CH���������£�
��CG��BH��G����ͼ2��ʾ��
ͬ��1���ã���BHC=45�㣬���CGH�ǵ���ֱ�������Σ���CH=![]() GH����CB=CE��CG��BE����BG=EG=
GH����CB=CE��CG��BE����BG=EG=![]() BE����BH+EH=BG+EG+EH+EH=2GH=
BE����BH+EH=BG+EG+EH+EH=2GH=![]() CH��
CH��
�ʴ�Ϊ��BH+EH=![]() CH��
CH��
��3����90�㣼����180�㣬�����������䣬��2���еĹ�ϵʽ��������BH��EH=![]() CH���������£�
CH���������£�
��CG��BH��G����ͼ3��ʾ��
ͬ��2���ã���BHC=45�㣬��CGH�ǵ���ֱ�������Σ�CH=![]() GH��BG=EG=
GH��BG=EG=![]() BE����BH��EH=BG+GH��EH=BG+EG��EH��EH=2GH=
BE����BH��EH=BG+GH��EH=BG+EG��EH��EH=2GH=![]() CH��
CH��



 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AE��BC������ΪE�����AB��5��AE��4��BC��8�������н��ۣ�
��DE��4![]() ��
��
��S��AED��![]() S�ı���ABCD��
S�ı���ABCD��
��DEƽ�֡�ADC��
�ܡ�AED����ADC��
������ȷ���۵������_____����������ȷ���۵���Ŷ����ں����ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�İ뾶Ϊ5��ֱ��l����O��A����ֱ��l��ȡ��B��AB=4��
��1�������̶ȵ�ֱ�ߺ�Բ�棬����B��ֱ��m��l������O��C��D����D�ڵ�C���Ϸ�������������ͼ�ۼ�����Ҫ��д������
��2����BC�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����з���û��ʵ�������ǣ�������
A. x3+2��0B. x2+2x+2��0
C. ![]() ��x��1D.
��x��1D. ![]() ��0
��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬AC��6��BC��8��D��E�ֱ�Ϊ��BC��AC��һ�㣬����ADE����ֱ��AD���ۣ���E���ڵ�F�������DF��BC����AEF�ǵȱ������Σ���ôAE��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����λ���ȣ�������![]() ���������㶼�ڸ����.
���������㶼�ڸ����.
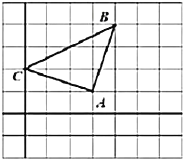
��1��������![]() Ϊԭ��
Ϊԭ��![]() ������ƽ��ֱ������ϵ����д��
������ƽ��ֱ������ϵ����д��![]() ��
��![]() ���������.
���������.
��2����������![]() �ڲ���һ��
�ڲ���һ��![]() ������ƽ�ƺ�Ķ�Ӧ��
������ƽ�ƺ�Ķ�Ӧ��![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ��
��![]() �Ķ�Ӧ��ֱ�Ϊ
�Ķ�Ӧ��ֱ�Ϊ![]() ��
��![]() ��
��![]() ����˵��������
����˵��������![]() �������������
�������������![]() ƽ�Ƶõ�����������ƽ�ƣ���������������
ƽ�Ƶõ�����������ƽ�ƣ���������������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ڽ����ڼ俪չ�Żݴ����������ԭ�۳���500Ԫ����Ʒ������500Ԫ�IJ��ֿ������ܴ����Żݣ���������Ʒ��ʵ�ʸ�����y(��λ��Ԫ)����Ʒԭ��x(��λ��Ԫ)�ĺ�����ϵ��ͼ����ͼ��ʾ����500Ԫ�IJ��ֿ������ܵ��Ż���( )

A. ������B. ������C. �����D. �����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����һ���߶�Ϊ�Խ����������Σ���Ƹ�������Ϊ�����߶ε����Խ����������������磬ͼ����������ABCD��Ϊ�߶�BD�����Խ���������������ͼ�ڣ��ڡ�ABC�У���ABC=90�㣬AB=3cm��BC=4cm����P�ӵ�C������������CA��AB��5cm/s���ٶ��˶�������P���B���غ�ʱ�����߶�PB�����Խ����������������P���˶�ʱ��Ϊt��s�����߶�PB�����Խ����������������ΪS��cm2����
��1����ͼ�ۣ��������ߵ�С�������������߶�AB�����Խ�������������
��2�����߶�PB�����Խ�����������������ͬʱ���ڡ�ABC�ı���ʱ����t��ֵ��
��3������P������CA��AB�˶�ʱ����S��t֮��ĺ�����ϵʽ��
��4���������˶������У����߶�PB�����Խ�����������������һ���������ڡ�A��ƽ������ʱ��ֱ��д��t��ֵ��



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����![]() �У�AB=AC����ABC =
�У�AB=AC����ABC =![]() ��D��BC����һ�㣬��ADΪ����
��D��BC����һ�㣬��ADΪ����![]() ��ʹAE=AD��
��ʹAE=AD��![]() +
+![]() =180����
=180����

��1��ֱ��д����ADE�Ķ������ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2����AB��AEΪ����ƽ���ı���ABFE��
����ͼ2������Fǡ������DE�ϣ���֤��BD=CD��
����ͼ3������Fǡ������BC�ϣ���֤��BD=CF��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com