
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D,E分别为边BC,AC上一点,将△ADE沿着直线AD翻折,点E落在点F处,如果DF⊥BC,△AEF是等边三角形,那么AE=_____.

【答案】4.
【解析】
由题意可得∠CAD=30°,∠AEF=60°,根据勾股定理可求CD=2![]() ,由AC∥DF,则∠AEF=∠EFD=60°,且DE=DF,可得∠DEF=∠DFE=60°,可得∠DEC=60°.根据勾股定理可求EC的长,即可求AE的长.
,由AC∥DF,则∠AEF=∠EFD=60°,且DE=DF,可得∠DEF=∠DFE=60°,可得∠DEC=60°.根据勾股定理可求EC的长,即可求AE的长.
如图:

∵折叠,
∴∠EAD=∠FAD,DE=DF,
∴∠DFE=∠DEF;
∵△AEF是等边三角形,
∴∠EAF=∠AEF=60°,
∴∠EAD=∠FAD=30°;
在Rt△ACD中,AC=6,∠CAD=30°,
∴CD=2![]() ;
;
∵FD⊥BC,AC⊥BC,
∴AC∥DF,
∴∠AEF=∠EFD=60°,
∴∠FED=60°;
∵∠AEF+∠DEC+∠DEF=180°,
∴∠DEC=60°;
∵在Rt△DEC中,∠DEC=60°,CD=2![]() ,
,
∴EC=2;
∵AE=AC﹣EC,
∴AE=6﹣2=4;
故答案为:4.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(1,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣
的图象的两个交点.、(1)求△AOB的面积;(2)求不等式kx+b﹣![]() <0的解集(请直接写出答案).
<0的解集(请直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A、B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),是否存在实数k使得直线y=kx+1与以O、C为直径的圆相切?若存在,请求出k的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P(1,m)、Q(n,1)在反比例函数y=![]() 的图象上,直线y=kx+b经过点P、Q,且与x轴、y轴的交点分别为A、B两点.
的图象上,直线y=kx+b经过点P、Q,且与x轴、y轴的交点分别为A、B两点.
(1)求 k、b的值;
(2)O为坐标原点,C在直线y=kx+b上且AB=AC,点D在坐标平面上,顺次联结点O、B、C、D的四边形OBCD满足:BC∥OD,BO=CD,求满足条件的D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-20,B点对应的数为80.

(1)请写出AB的中点M对应的数.
(2)现在有一只电子蚂蚁P从B点出发,以2个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以3个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,
①你知道经过几秒两只电子蚂蚁相遇?
②点C对应的数是多少?
③经过多长时间两只电子蚂蚁在数轴上相距15个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD为正方形,将正方形的边CB绕点C顺时针旋转到CE,记∠BCE=α,连接BE,DE,过点C作CF⊥DE于F,交直线BE于H.
(1)当α=60°时,如图1,则∠BHC= ;
(2)当45°<α<90°,如图2,线段BH、EH、CH之间存在一种特定的数量关系,请你通过探究,写出这个关系式: (不需证明);
(3)当90°<α<180°,其它条件不变(如图3),(2)中的关系式是否还成立?若成立,说明理由;若不成立,写出你认为成立的结论,并简要证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区举行“中华诵![]() 经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图
经典诵读”大赛,小学、中学组根据初赛成绩,各选出5名选手组成小学代表队和中学代表队参加市级决赛,两个代表队各选出的5名选手的决赛成绩分别绘制成下列两个统计图

根据以上信息,整理分析数据如下:
平均数(分 | 中位数(分 | 众数(分 | |
小学组 | 85 |
| 100 |
中学组 |
| 85 |
|
(1)写出表格中![]() ,
,![]() ,
,![]() 的值:
的值:![]() ,
,![]() ,
,![]() .
.
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在平面直角坐标系中,![]() 、
、![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足关系式
满足关系式![]() ,平移
,平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() .
.
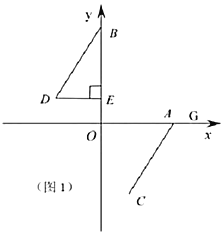
(1)直接写出![]() 、
、![]() 两点的坐标,则
两点的坐标,则![]() (______,______)、
(______,______)、![]() (______,______).
(______,______).
(2)如图1,过点![]() 作
作![]() 轴交于
轴交于![]() 点,猜想
点,猜想![]() 与
与![]() 数量关系,并说明理由.
数量关系,并说明理由.
(3)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 点,
点,![]() 为
为![]() 轴上点
轴上点![]() 左侧的一动点,连接
左侧的一动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,当点
,当点![]() 运动时,
运动时,![]() 的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
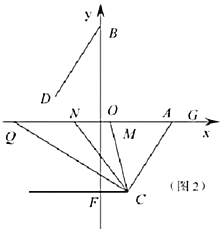
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是_________(用代数式表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com