
【题目】如图1所示,在平面直角坐标系中,![]() 、
、![]() 、
、![]() ,其中
,其中![]() 、
、![]() 满足关系式
满足关系式![]() ,平移
,平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() .
.
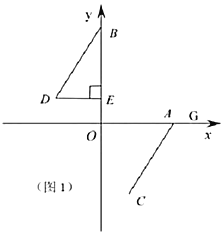
(1)直接写出![]() 、
、![]() 两点的坐标,则
两点的坐标,则![]() (______,______)、
(______,______)、![]() (______,______).
(______,______).
(2)如图1,过点![]() 作
作![]() 轴交于
轴交于![]() 点,猜想
点,猜想![]() 与
与![]() 数量关系,并说明理由.
数量关系,并说明理由.
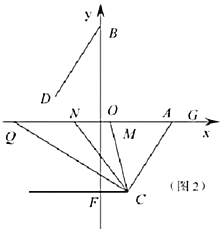
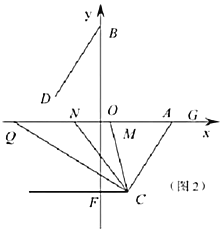
(3)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 点,
点,![]() 为
为![]() 轴上点
轴上点![]() 左侧的一动点,连接
左侧的一动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,当点
,当点![]() 运动时,
运动时,![]() 的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
的值是否变化?如果变化,请说明理由;如果不变,请求出其值.
【答案】(1)3;0;-2;1;(2)互补,理由见解析;(3)不变;![]() .
.
【解析】
(1)根据算术平方根的非负性和平方的非负性即可求出a、b的值,从而求出A、B的坐标,再根据A、B的坐标即可发现点A到点B的平移规律,从而得到:点C到点D的平移规律,即可求出D点坐标;
(2)延长DE和CA交于点P,根据平行线的性质即可证出:![]() =∠P=∠OAC,然后根据平角的定义即可得:∠OAC+∠CAG=180°,从而得到:
=∠P=∠OAC,然后根据平角的定义即可得:∠OAC+∠CAG=180°,从而得到:![]() 与
与![]() 互补;
互补;
(3)根据角平分线的定义可得:∠ACM=![]() ,∠ACN=
,∠ACN=![]() ,从而得出∠MCN=∠ACN-∠ACM=
,从而得出∠MCN=∠ACN-∠ACM=![]() ,再根据平行线的性质可得:∠AQC=∠FCQ,即可求出
,再根据平行线的性质可得:∠AQC=∠FCQ,即可求出![]() 的值.
的值.
解:(1)∵![]()
∴![]()
解得:![]()
∴点A坐标为:(3,0),点B的坐标为:(0,4)
∵平移![]() 使点
使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点为点
的对应点为点![]() ,
,
由坐标可知:点A到点B的平移规律为:先向左平移3个单位,再向上平移4个单位
∴点C到点D的平移规律为:先向左平移3个单位,再向上平移4个单位
∴点D的坐标为:(1-3,﹣3+4)=(-2,1);
(2)互补,理由如下,
延长DE和CA交于点P,如下图所示
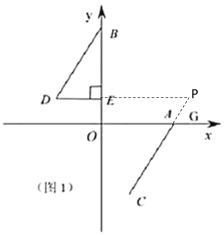
∵BD∥CA
∴![]() =∠P
=∠P
∵DE⊥y轴
∴DE∥x轴
∴![]() =∠P=∠OAC
=∠P=∠OAC
∵∠OAC+∠CAG=180°
∴![]() +∠CAG=180°
+∠CAG=180°
∴![]() 与
与![]() 互补;
互补;
(3)不变,
∵![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴∠ACM=![]() ,∠ACN=
,∠ACN=![]() ,
,
∴∠MCN=∠ACN-∠ACM=![]() -
-![]() =
=![]() =
=![]() ,
,
∵![]() 轴,
轴,
∴∠AQC=∠FCQ,
∴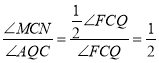 .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】从2012年7月1日起某市执行新版居民阶梯电价,小明同学家收到了新政后的第一张电费单,小明爸爸说:“小明,请你计算一下,这个月的电费支出与新政前相比是多了还是少了?”于是小明上网了解了有关电费的收费情况,得到如下两表:
2004年1月至2012年6月执行的收费标准:
月用电量(度)50度有以下部分 | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
单价(元/度) | 0.53 | 0.56 | 0.63 |
2012年7月起执行的收费标准:
月用电量(度) | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
单价(元/度) | 0.53 | 0.58 | 0.83 |
(1)若小明家2012年7月份的用电量为200度,则小明家7月份的电费支出是多少元?比新政前少了多少元?
(2)若新政后小明家的月用电量为a度,请你用含a的代数式表示当月的电费支出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.D,E分别为边BC,AC上一点,将△ADE沿着直线AD翻折,点E落在点F处,如果DF⊥BC,△AEF是等边三角形,那么AE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图像如图所示,则超过500元的部分可以享受的优惠是( )

A. 打六折B. 打七折C. 打八折D. 打九折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:两个观察者从A,B两地观测空中C处一个气球,分别测得仰角为45°和60°,已知A,B两地相距200m,当气球沿着与AB平行地漂移40秒后到达C1,在A处测得气球的仰角为30度.
求:(1)气球漂移的平均速度(结果保留3个有效数字);
(2)在B处观测点C1的仰角(精确到度).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作平行四边形ABCD的边AB的中点”的尺规作图过程.
已知:平行四边形ABCD.
求作:点M,使点M 为边AB 的中点.
作法:如图,
①作射线DA;
②以点A 为圆心,BC长为半径画弧,
交DA的延长线于点E;
③连接EC 交AB于点M .
所以点M 就是所求作的点.

根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,EB.
∵四边形ABCD 是平行四边形,
∴AE∥BC.
∵AE= ,
∴四边形EBCA 是平行四边形( )(填推理的依据) .
∴AM =MB ( )(填推理的依据) .
∴点M 为所求作的边AB的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
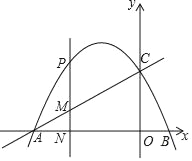
【题目】如图,抛物线y=﹣![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3交x轴负半轴于点A,交y轴于点C,交x轴正半轴于点B.
x+3交x轴负半轴于点A,交y轴于点C,交x轴正半轴于点B.
(1)求抛物线的解析式;
(2)点P为抛物线上任意一点,设点P的横坐标为x.
①若点P在第二象限,过点P作PN⊥x轴于N,交直线AC于点M,求线段PM关于x的函数解析式,并求出PM的最大值;
②若点P是抛物线上任意一点,连接CP,以CP为边作正方形CPEF,当点E落在抛物线的对称轴上时,请直接写出此时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com