
����Ŀ����ͼ��������y=��![]() x2+bx+c��ֱ��y=
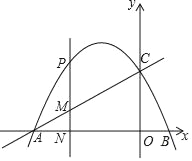
x2+bx+c��ֱ��y=![]() x+3��x�Ḻ�����ڵ�A����y���ڵ�C����x���������ڵ�B��
x+3��x�Ḻ�����ڵ�A����y���ڵ�C����x���������ڵ�B��
��1���������ߵĽ���ʽ��
��2����PΪ������������һ�㣬���P�ĺ�����Ϊx��
������P�ڵڶ����ޣ�����P��PN��x����N����ֱ��AC�ڵ�M�����߶�PM����x�ĺ�������ʽ�������PM�����ֵ��
������P��������������һ�㣬����CP����CPΪ����������CPEF������E���������ߵĶԳ�����ʱ����ֱ��д����ʱ��P�����꣮
���𰸡���1�������߽���ʽΪy=��![]() x2��
x2��![]() x+3����2���ٵ�x=��2ʱ���߶�PM�ij������ֵ�����ֵΪ
x+3����2���ٵ�x=��2ʱ���߶�PM�ij������ֵ�����ֵΪ![]() ����P������Ϊ����4��0����
����P����������4��0����![]() ��
��![]() ����2��0����
����2��0����![]() ��
��![]() ����
����
�������������������1������һ�κ�������ʽȷ����C��0��3����A����4��0����Ȼ�����ô���ϵ����ȷ�������߽���ʽ��
��2������P��x����![]() x2��
x2��![]() x+3������4��x��0������M��x��
x+3������4��x��0������M��x��![]() x+3������PM=��
x+3������PM=��![]() x2��
x2��![]() x+3����
x+3����![]() x+3����Ȼ����ݶ��κ��������ʽ��������
x+3����Ȼ����ݶ��κ��������ʽ��������
����PK��y����K���������ߵĶԳ�����G����ͼ����֤����PEG�ա�CPK�õ�CK=PG����P��x����![]() x2��
x2��![]() x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����
x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����![]() x2��
x2��![]() x+3����K��0����
x+3����K��0����![]() x2��
x2��![]() x+3������PG=|��1��x|=|x+1|��CK=|��
x+3������PG=|��1��x|=|x+1|��CK=|��![]() x2��
x2��![]() x+3��3|=|��
x+3��3|=|��![]() x2��
x2��![]() x|������|x+1|=|��
x|������|x+1|=|��![]() x2��
x2��![]() x|��Ȼ������ֵ�������x���Ӷ��õ�����������P�����꣮
x|��Ȼ������ֵ�������x���Ӷ��õ�����������P�����꣮
���������������1����x=0ʱ��y=![]() x+3=3����C��0��3����
x+3=3����C��0��3����
��y=0ʱ��![]() x+3=0�������x=��4����A����4��0������A����4��0����C��0��3������y=��
x+3=0�������x=��4����A����4��0������A����4��0����C��0��3������y=��![]() x2+bx+c����
x2+bx+c����![]() �������
�������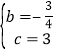 ���������߽���ʽΪy=��
���������߽���ʽΪy=��![]() x2��
x2��![]() x+3��
x+3��
��2������P��x����![]() x2��
x2��![]() x+3������4��x��0������M��x��
x+3������4��x��0������M��x��![]() x+3������PM=��
x+3������PM=��![]() x2��
x2��![]() x+3����
x+3����![]() x+3��=��
x+3��=��![]() x2��
x2��![]() x=��
x=��![]() ��x+2��2+
��x+2��2+![]()
��x=��2ʱ���߶�PM�ij������ֵ�����ֵΪ![]() ��
��
����PK��y����K���������ߵĶԳ�����G����ͼ�����ı���PEFCΪ����������PE=PC����EPC=90�㣮�ߡ�PGE=��PKC=90�㣬���PEG=��CPK���á�PEG�ա�CPK����CK=PG����P��x����![]() x2��
x2��![]() x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����
x+3���������ߵĶԳ���Ϊֱ��x=��1����G����1����![]() x2��
x2��![]() x+3����K��0����
x+3����K��0����![]() x2��
x2��![]() x+3������PG=|��1��x|=|x+1|��CK=|��
x+3������PG=|��1��x|=|x+1|��CK=|��![]() x2��
x2��![]() x+3��3|=|��
x+3��3|=|��![]() x2��
x2��![]() x|����|x+1|=|��
x|����|x+1|=|��![]() x2��
x2��![]() x|���ⷽ��x+1=��
x|���ⷽ��x+1=��![]() x2��
x2��![]() x����x1=��4��x2=��
x����x1=��4��x2=��![]() ��
��
�ⷽ��x+1=![]() x2+
x2+![]() x����x1=2��x2=��
x����x1=2��x2=��![]() ��
��
��P����������4��0����![]() ����2��0����
����2��0����![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
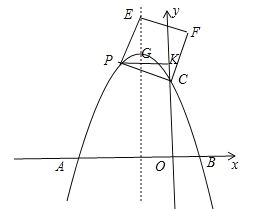
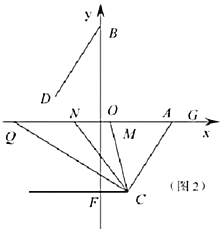
����Ŀ����ͼ1��ʾ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() �����ϵʽ
�����ϵʽ![]() ��ƽ��
��ƽ��![]() ʹ��
ʹ��![]() ���
���![]() �غϣ���
�غϣ���![]() �Ķ�Ӧ��Ϊ��
�Ķ�Ӧ��Ϊ��![]() .
.
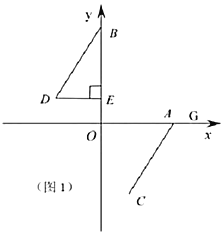
��1��ֱ��д��![]() ��
��![]() ��������꣬��
��������꣬��![]() ��______��______����
��______��______����![]() ��______��______��.
��______��______��.
��2����ͼ1������![]() ��
��![]() �ύ��
�ύ��![]() �㣬����
�㣬����![]() ��
��![]() ������ϵ����˵������.
������ϵ����˵������.
��3����ͼ2������![]() ��
��![]() �ύ
�ύ![]() ����
����![]() �㣬
�㣬![]() Ϊ
Ϊ![]() ���ϵ�
���ϵ�![]() ����һ���㣬����
����һ���㣬����![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() ������
������![]() �˶�ʱ��
�˶�ʱ��![]() ��ֵ�Ƿ�仯������仯����˵�����ɣ�������䣬�������ֵ.
��ֵ�Ƿ�仯������仯����˵�����ɣ�������䣬�������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������״��С��ȫ��ͬ��С�����ο�Ƭ����ͼ�٣����ص��ط���һ������Ϊ�����Σ���Ϊm����Ϊn���ĺ��ӵײ�����ͼ�ڣ������ӵײ�δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ����������Ӱ�����ܳ�����_________���ô���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ��2019��4��10�������״�ֱ�����㵽�ڶ�����Ƭ������һ���������͡������ڶ���λ����Ů����ϵ����һ������������ϵ��M87�����ģ��������5500����꣮���ݡ�5500����ꡱ�ÿ�ѧ��������ʾΪ(����)

A.5500��104����B.055��108����
C.5.5��103����D.5.5��107����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
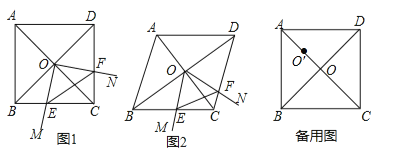
����Ŀ����12�֣�����ABCD�У������Խ���AC��BD�ཻ�ڵ�O����MON+��BCD=180�㣬��MON�Ƶ�O��ת������OM����BC�ڵ�E������ON����DC�ڵ�F������EF��
��1����ͼ1������ABC=90��ʱ����OEF����״�� ��
��2����ͼ2������ABC=60��ʱ�����ж���OEF����״����˵�����ɣ�
��3���ڣ�1���������£�����MON�Ķ����Ƶ�AO���е�O�䴦����MO��N�Ƶ�O����ת����������MO��N+��BCD=180�㣬����O��M��ֱ��BC�ڵ�E������O��N��ֱ��CD�ڵ�F����BC=4����![]() ʱ��ֱ��д���߶�CE�ij���
ʱ��ֱ��д���߶�CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�ֹ�������У��ס������˽ӵ��ֹ�����ֽ��������֪��ÿСʱ����ֽ������ÿСʱ����ֽ����20�䣬������120��ֽ����ʱ����������160��ֽ����ʱ����ͬ
(1)��ס�������ÿСʱ������ֽ�����ٶ䣿
(2)���λѧУ��Ҫ����ֽ��������350�䣬���ɼס������˹�ͬ��������������Ҫ��Сʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
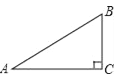
����Ŀ��ijУ�ƻ���һ�������ֱ�������εķϵؿ���Ϊ��������ͼ��ʾ����ACB=90�㣬BC=60������A=36�㣮
��1������ڴ�E��AB����������A��B�Ⱦ�������CE�ij�����ȷ����λ����
��2����D����AB�������ƻ����߶�CD��һ��ˮ������֪ˮ�������Ϊ50Ԫ/����ˮ��·��Ӧ�����Ʋ���ʹ�������������������
������sin36��=0.5878��cos36��=0.8090��tan36��=0.7265��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����x�����������A��B�ĺ�����ֱ�Ϊ��3��1����y�ύ�ڵ�C�������ĸ����ۣ���16a+4b+c��0������P����5��y1����Q��![]() ��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��
��y2���Ǻ���ͼ���ϵ����㣬��y1��y2����c=��3a��������ABC�ǵ��������Σ���b=��![]() ��
��![]() ��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
��������ȷ����_____�����뽫��ȷ���۵����ȫ�����ں����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������ACΪֱ������O����AB��D������O��OE��AB����BC��E��
��1����֤��EDΪ��O�����ߣ�
��2�������O�İ뾶Ϊ![]() ��ED=2���ӳ�EO����O��F������DF��AF������ADF�������
��ED=2���ӳ�EO����O��F������DF��AF������ADF�������

���𰸡���1��֤������������2��![]()
�������������������1����������OD����OE��AB������ƽ��������������ε����ʣ���֤��![]() ��
��![]() ���ɵ�
���ɵ�![]() �����֤��
�����֤��![]() Ϊ
Ϊ![]() �����ߣ�
�����ߣ�
��2������CD������ֱ�����Ե�Բ�ܽ���ֱ�ǣ����ɵ�![]() ���ù��ɶ����������
���ù��ɶ����������![]() �ij�������OE��AB��֤��
�ij�������OE��AB��֤��![]() �������������εĶ�Ӧ�߳ɱ������������
�������������εĶ�Ӧ�߳ɱ������������![]() �ij���Ȼ���������Ǻ�����֪ʶ�����
�ij���Ȼ���������Ǻ�����֪ʶ�����![]() ��
��![]() �ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
�ij���Ȼ������S��ADF=S����ABEF-S����DBEF��ô𰸣�
���������(1)֤��������OD��

��OE��AB��
���COE=��CAD����EOD=��ODA��
��OA=OD,
���OAD=��ODA��
���COE=��DOE��
�ڡ�COE�͡�DOE�У�
 ���COE�ա�DOE(SAS)��
���COE�ա�DOE(SAS)��
![]()
��ED��OD��
��ED��![]() �����ߣ�
�����ߣ�
(2)����CD����OE��M��
��Rt��ODE��
��OD=32��DE=2��
![]()
��OE��AB��
���COE�ס�CAB��
![]() ��AB=5��
��AB=5��
��AC��ֱ����
![]()
![]()
![]()
![]()
��EF��AB��
![]()
![]()
![]()
��S��ADF=S����ABEFS����DBEF
![]()
���ADF�����Ϊ![]()

�����͡������
��������
25
����Ŀ������Ŀ����֪��������y=ax2+ax+b��a��0����ֱ��y=2x+m��һ��������M��1��0������a��b��
��1����b��a�Ĺ�ϵʽ�������ߵĶ���D���꣨��a�Ĵ���ʽ��ʾ����
��2��ֱ���������ߵ�����һ�������ΪN������DMN�������a�Ĺ�ϵʽ��
��3��a=��1ʱ��ֱ��y=��2x���������ڵڶ������ڵ�G����G��H����ԭ��Գƣ��ֽ��߶�GH��y������ƽ��t����λ��t��0�������߶�GH����������������ͬ�Ĺ����㣬����t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com