
ЁОЬтФПЁПвбжЊЃКШчЭМ1ЃЌЕуOЪЧжБЯпABЩЯвЛЕуЃЌЙ§ЕуOзїЩфЯпOC.
(1)ШєЁЯAOC=140ЁуЃЌдђЁЯBOC=________Ёу.
(2)дкЭМ1жаЗжБ№ЛЁЯAOCЕФНЧЦНЗжЯпOEКЭЁЯBOCЕФНЧЦНЗжЯпOFЃЌФЧУД,OEКЭOFгаЪВУДЮЛжУЙиЯЕЃЌЧыЫЕУїРэгЩ.
(3)ШєЁЯBOC=30ЁуЃЌЩфЯпODДгOBГіЗЂЃЌШЦЕуOвдУПУы10ЁуНЧЕФЫйЖШФцЪБеыа§зЊ.ЕБЩфЯпODгыЩфЯпOAжиКЯЪБЃЌЩфЯпOCвдУПУы30ЁуНЧЕФЫйЖШШЦЕуOФцЪБеыа§зЊЃЌЩфЯпODАДдРДЕФЫйЖШКЭЗНЯђМЬаја§зЊЃЌЕБЩфЯпOCЛђЩфЯпODжагавЛЬѕЩфЯпгыЩфЯпOBжиКЯЪБЃЌСНЬѕЩфЯпЖМЭЃжЙ.ЩшЩфЯпODа§зЊЕФЪБМфЮЊtУыЃЌдка§зЊЕФЙ§ГЬжаЃЌЪЧЗёДцдкФГИіЪБПЬЃЌЪЙЕУЩфЯпOBЁЂOCгыODжаЕФФГвЛЬѕЩфЯпЪЧСэСНЬѕЩфЯпЫљМаНЧЕФЦНЗжЯп?ШєДцдкЃЌжБНгаДГіЫљгаТњзуЬѕМўЕФtЕФжЕЃЌШєВЛДцдкЃЌЫЕУїРэгЩ.
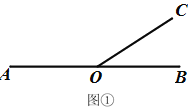
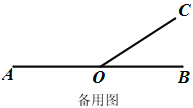
ЁОД№АИЁПЃЈ1ЃЉ40ЃЛЃЈ2ЃЉEOЁЭFOЃЌРэгЩМћНтЮіЃЈ3ЃЉt=1.5sЛђ6s
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнСкВЙНЧМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнНЧЦНЗжЯпгыДЙжБЕФЖЈвхМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЗжЩфЯпODЪЧЩфЯпOBЁЂЩфЯпOCЕФНЧЦНЗжЯпЃЛЩфЯпOCЪЧЩфЯпODЁЂЩфЯпOBЕФНЧЦНЗжЯпЃЛЩфЯпOBЪЧЩфЯпODЁЂЩфЯпOCЕФНЧЦНЗжЯпЗжБ№ЬжТлМДПЩЧѓНт.
ЃЈ1ЃЉЁпЁЯAOC=140ЁуЃЌдђЁЯBOC=180Ёу-ЁЯAOC=40ЁуЃЌ
ЙЪЬюЃК40ЃЛ
ЃЈ2ЃЉEOЁЭFOЃЌРэгЩШчЯТЃК
ШчЭМЃКЁпOEЪЧЁЯAOCЕФНЧЦНЗжЯпЃЌOFЪЧЁЯBOCЕФНЧЦНЗжЯпЃЌ
ЁрЁЯCOE=![]() ЁЯAOCЃЌЁЯCOF=
ЁЯAOCЃЌЁЯCOF=![]() ЁЯBOCЃЌ
ЁЯBOCЃЌ
ЁрЁЯCOE+ЁЯCOF=![]() ЁЯAOC+
ЁЯAOC+![]() ЁЯBOC=
ЁЯBOC=![]() (ЁЯAOC+ЁЯBOC)=
(ЁЯAOC+ЁЯBOC)=![]() ЁС180Ёу=90ЁуЃЌ
ЁС180Ёу=90ЁуЃЌ
МДЁЯEOF=90ЁуЃЌ
ЁрEOЁЭFO.
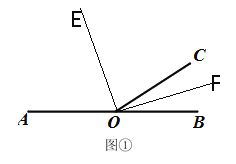
ЃЈ3ЃЉгЩЬтвтЕУЕБODдЫЖЏЕНOAЪБЃЌt=18sЃЌЕБODдЫЖЏЕНOBЪБЃЌt=36s,ЕБOCдЫЖЏЕНOBЪБЃЌt=18+330ЁТ30=29s,
ЂйЩфЯпODЪЧЩфЯпOBЁЂЩфЯпOCЕФНЧЦНЗжЯпЪБЃЌ
ЕБODдЫЖЏЃЌOCВЛЖЏЪБЃЌ0ЃМtЃМ18ЃЌ
ЁпЁЯBOC=30ЁуЃЌ
ЁрЁЯBOD=![]() ЁЯBOC=15ЁуЃЌ
ЁЯBOC=15ЁуЃЌ
ЙЪt=15ЁТ10=1.5s
ЕБODдЫЖЏЃЌOCвВдЫЖЏЪБЃЌ18ЃМtЃМ29,
ЁЯBOD=360Ёу-10t,ЁЯBOC=360Ёу-30-30ЃЈt-18ЃЉ
ЁпЁЯBOD=![]() ЁЯBOC
ЁЯBOC
Ёр360Ёу-10t=![]() [360Ёу-30-30ЃЈt-18ЃЉ]
[360Ёу-30-30ЃЈt-18ЃЉ]
НтЕУt=15s,ВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЂкЩфЯпOCЪЧЩфЯпODЁЂЩфЯпOBЕФНЧЦНЗжЯпЪБ
ЕБODдЫЖЏЃЌOCВЛЖЏЪБЃЌ0ЃМtЃМ18ЃЌ
ЁпЁЯBOC=30ЁуЃЌ
ЁрЁЯBOD=2ЁЯBOC=60ЁуЃЌt=60ЁТ10=6s;
ЕБODдЫЖЏЃЌOCвВдЫЖЏЪБЃЌ18ЃМtЃМ29,
ЩфЯпOCдкЩфЯпOBгыЩфЯпODЫљМаЖлНЧжЎМфЃЌВЛЗћКЯЬтвтЃЛ
ЂлЩфЯпOBЪЧЩфЯпODЁЂЩфЯпOCЕФНЧЦНЗжЯп
ВЛДцдкЕБODдЫЖЏЃЌOCВЛЖЏЕФЧщПіЃЛ
ЕБODдЫЖЏЃЌOCвВдЫЖЏЪБЃЌ18ЃМtЃМ29,
ЩфЯпOBдкЩфЯпOCгыЩфЯпODЫљМаЖлНЧжЎМфЃЌВЛЗћКЯЬтвт
злЩЯЃЌt=1.5sЛђ6sЪБЃЌЪЙЕУЩфЯпOBЁЂOCгыODжаЕФФГвЛЬѕЩфЯпЪЧСэСНЬѕЩфЯпЫљМаНЧЕФЦНЗжЯп.


 МтзгЩњаТПЮЬУПЮЪБзївЕЯЕСаД№АИ
МтзгЩњаТПЮЬУПЮЪБзївЕЯЕСаД№АИ гЂВХМЦЛЎЭЌВНПЮЪБИпаЇбЕСЗЯЕСаД№АИ
гЂВХМЦЛЎЭЌВНПЮЪБИпаЇбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЯТЭМЃЌНЋвЛеХе§ЗНаЮжНЦЌЃЌМєГЩЫФИіДѓаЁаЮзДвЛбљЕФаЁе§ЗНаЮЃЌШЛКѓНЋЦфжаЕФвЛИіаЁе§ЗНаЮдйАДЭЌбљЕФЗНЗЈМєГЩЫФИіаЁе§ЗНаЮЃЌдйНЋЦфжаЕФвЛИіаЁе§ЗНаЮМєГЩЫФИіаЁе§ЗНаЮЃЌШчДЫбЛЗЯТШЅЃЎ
ЃЈ1ЃЉЬюаДЯТБэЃК
МєЕФДЮЪ§ | 1 | 2 | 3 | 4 | 5 |
е§ЗНаЮИіЪ§ | 4 | 7 | 10 | ЁЁ ЁЁ | ЁЁ ЁЁ |
ЃЈ2ЃЉШчЙћМєСЫ8ДЮЃЌЙВМєГіЁЁ ЁЁИіаЁе§ЗНаЮЃЎ
ЃЈ3ЃЉШчЙћМєnДЮЃЌЙВМєГіЁЁ ЁЁИіаЁе§ЗНаЮЃЎ
ЃЈ4ЃЉЩшзюГѕе§ЗНаЮжНЦЌЮЊ1ЃЌдђМєnДЮКѓЃЌзюаЁе§ЗНаЮЕФБпГЄЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпl1ЕФНтЮіБэДяЪНЮЊy=-3x+3ЃЌЧвl1гыxжсНЛгкЕуDЃЌжБЯпl2ОЙ§ЕуAЃЌBЃЌжБЯпl1ЃЌl2ЃЌНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЧѓжБЯпl2ЕФНтЮіБэДяЪНЃЛ
ЃЈ3ЃЉЧѓЁїADCЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввЁЂБћШ§ШЫзМБИЭцДЋЧђгЮЯЗЃЎЙцдђЪЧЃКЕк1ДЮДЋЧђДгМзПЊЪМЃЌМзЯШНЋЧђЫцЛњДЋИјввЁЂБћСНШЫжаЕФвЛИіШЫЃЌдйгЩНгЕНЧђЕФШЫЫцЛњДЋИјЦфЫћСНШЫжаЕФвЛИіШЫЁШчДЫЗДИДЃЎ
ЃЈ1ЃЉШєДЋЧђ1ДЮЃЌЧђдкввЪжжаЕФИХТЪЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєДЋЧђ3ДЮЃЌЧѓЧђдкМзЪжжаЕФИХТЪЃЈгУЪїзДЭМЛђСаБэЗЈЧѓНтЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаИїЪНЃК
13ЃН![]() ЁС12ЁС22
ЁС12ЁС22
13+23ЃН9ЃН![]() ЁС22ЁС32
ЁС22ЁС32
13+23+33ЃН36ЃН![]() ЁС32ЁС42
ЁС32ЁС42
13+23+33+43ЃН100ЃН![]() ЁС42ЁС52
ЁС42ЁС52
ЛиД№ЯТУцЕФЮЪЬтЃК
(1)ВТЯыЃК13+23+33+Ё+(nЃ1)3+ n3ЃН________.
(2)РћгУФуЕУЕНЕФ(1)жаЕФНсТлЃЌМЦЫу13+23+33+Ё+993+1003ЕФжЕ.
(3)МЦЫуЃК213+223+Ё+993+1003ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФИЧзНкЕНСЫЃЌаЁУїзМБИЮЊТшТшжѓЫФИіДѓЬРдВзїдчЕуЃКвЛИіжЅТщЯкЃЌвЛИіХЃШтЯкЃЌСНИіЛЈЩњЯкЃЌЫФИіЬРдВГ§ФкВПЯкСЯВЛЭЌЭтЃЌЦфЫќвЛЧаОљЯрЭЌЃЎ
ЃЈ1ЃЉЗжБ№гУAЃЌBЃЌCБэЪОжЅТщЯкЁЂХЃШтЯкЁЂЛЈЩњЯкЕФДѓЬРдВЃЌЧѓТшТшГдЧАСНИіЬРдВИеКУЖМЪЧЛЈЩњЯкЕФИХТЪЃЈЧыгУЁАЛЪїзДЭМЁБЛђЁАСаБэЁБЕШЗНЗЈЃЌаДГіЗжЮіЙ§ГЬЃЌВЂИјГіНсЙћЃЉЃЛ
ЃЈ2ЃЉШєЛЈЩњЯкЕФДѓЬРдВЕФИіЪ§ЮЊnИіЃЈnЁн2ЃЉЃЌдђТшТшГдЧАСНИіЬРдВЖМЪЧЛЈЩњЯкЕФИХТЪЪЧ ЃЈЧыгУКЌnЕФЪНзгжБНгаДГіНсЙћЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=mx2Љ2mx+nЃЈmЃМ0ЃЉЕФЖЅЕуЮЊAЃЌгыxжсНЛгкBЃЌCСНЕуЃЈЕуBдкЕуCзѓВрЃЉЃЌгыyжсе§АыжсНЛгкЕуDЃЌСЌНгADВЂбгГЄНЛxжсгкEЃЌСЌACЁЂDCЃЎSЁїDECЃКSЁїAEC=3ЃК4ЃЎ
ЃЈ1ЃЉЧѓЕуEЕФзјБъЃЛ
ЃЈ2ЃЉЁїAECФмЗёЮЊжБНЧШ§НЧаЮЃПШєФмЃЌЧѓГіДЫЪБХзЮяЯпЕФКЏЪ§БэДяЪНЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊСЫУРЛЏЛЗОГЃЌМЦЛЎдквЛЖЈЕФЪБМфФкЭъГЩТЬЛЏУцЛ§![]() ЭђФЖЕФШЮЮёЃЌКѓРДЪаеўИЎЕїећСЫдЖЈМЦЛЎЃЌВЛЕЋТЬЛЏУцЛ§вЊдкдМЦЛЎЕФЛљДЁЩЯдіМг
ЭђФЖЕФШЮЮёЃЌКѓРДЪаеўИЎЕїећСЫдЖЈМЦЛЎЃЌВЛЕЋТЬЛЏУцЛ§вЊдкдМЦЛЎЕФЛљДЁЩЯдіМг![]() ЃЌЖјЧввЊЬсЧА
ЃЌЖјЧввЊЬсЧА![]() ФъЭъГЩШЮЮёЃЌОВтЫувЊЭъГЩаТЕФМЦЛЎЃЌЦНОљУПФъЕФТЬЛЏУцЛ§БиаыБШдМЦЛЎЖр
ФъЭъГЩШЮЮёЃЌОВтЫувЊЭъГЩаТЕФМЦЛЎЃЌЦНОљУПФъЕФТЬЛЏУцЛ§БиаыБШдМЦЛЎЖр![]() ЭђФЖЃЌЧѓдМЦЛЎЦНОљУПФъЕФТЬЛЏУцЛ§ЃЎ
ЭђФЖЃЌЧѓдМЦЛЎЦНОљУПФъЕФТЬЛЏУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌЁЯAOBЪЧЦННЧЃЌЁЯAOCЃН30ЁуЃЌЁЯBODЃН60ЁуЃЌOMЃЌONЗжБ№ЪЧЁЯAOCЃЌЁЯBODЕФЦНЗжЯпЃЌЁЯMONЕШгк________.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com