[题目]甲.乙.丙三人准备玩传球游戏．规则是:第1次传球从甲开始.甲先将球随机传给乙.丙两人中的一个人.再由接到球的人随机传给其他两人中的一个人-如此反复．(1)若传球1次.球在乙手中的概率为 ,(2)若传球3次.求球在甲手中的概率．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】甲、乙、丙三人准备玩传球游戏．规则是：第1次传球从甲开始，甲先将球随机传给乙、丙两人中的一个人，再由接到球的人随机传给其他两人中的一个人…如此反复．

（1）若传球1次，球在乙手中的概率为　　；

（2）若传球3次，求球在甲手中的概率（用树状图或列表法求解）．

【答案】（1）（2）

【解析】试题分析：（1）若传球1次，球有可能在乙手中，也有可能在丙手中，所以球在乙手中的概率为．
（2）若传球3次，应用树状图法，求出球在甲手中的概率是多少即可．

试题解析：（1）∵传球1次，球有可能在乙手中，也有可能在丙手中，

∴球在乙手中的概率为．

（2）画出树状图如图所示：

∵3次传球后，所有等可能的情况共有8种，其中球在甲手中的有2种情况，

∴若传球3次，求球在甲手中的概率是：

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】计算:

(1) (-8)-47+18-(-27)

（2）-；
（3）12-（-18）+（-7）-15；
（4）4.7-（-8.9）-7.5+（-6）；
（5）(4；

(6)

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】定义：如图①，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于A，B两点，点P在该抛物线上(P点与A、B两点不重合)．如果△ABP的三边满足AP2＋BP2＝AB2，则称点P为抛物线y＝ax2＋bx＋c(a≠0)的勾股点．

(1)直接写出抛物线y＝－x2＋1的勾股点的坐标．

(2)如图②，已知抛物线y＝ax2＋bx(a≠0)与x轴交于A，B两点，点P(1， )是抛物线的勾股点，求抛物线的函数表达式．

(3)在(2)的条件下，点Q在抛物线上，求满足条件S△ABQ＝S△ABP的Q点(异于点P)的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某景区的三个景点A、B、C在同一线路上．甲、乙两名游客从景点A出发，甲步行到景点C;乙乘景区观光车先到景点B，在B处停留一段时间后，再步行到景点C，甲、乙两人同时到达景点C．甲、乙两人距景点A的路程y(米)与甲出发的时间x(分)之间的函数图象如图所示．

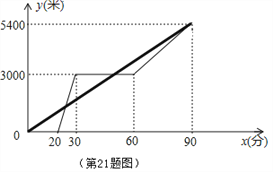
（1）乙步行的速度为_ __米/分．

（2）求乙乘景区观光车时y与x之间的函数关系式．

（3）甲出发多长时间与乙第一次相遇?

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某校为更好的开展“春季趣味运动会”活动，随机在各年级抽查了部分学生，了解他们最喜爱的趣味运动项目类型（跳绳、实心球、50m、拔河共四类），并将统计结果绘制成如下不完整的频数分布表（如图所示）

根据以上信息回答下列问题：

最喜爱的趣味运动项目类型频数分布表：

项目类型	频数	频率
跳绳	25	a
实心球	20
50m	b	0.4
拔河		0.15

（1）直接写出a=　　，b=　　；

（2）将图中的扇形统计图补充完整（注明项目、百分比）；

（3）若全校共有学生1200名，估计该校最喜爱50m和拔河的学生共约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示的方格纸中，每小方格的边长都为1.请在方格纸上画图并回容问题：已知点A、B.

(1)画直线AB，射线BC；

(2)过点C作垂线段CD⊥AB，垂足为点D.

(3)连结AC，则△ABC的面积＝_______.

(4)已知AB=5，求线段CD的长.

查看答案和解析>>

科目：初中数学 来源： 题型：

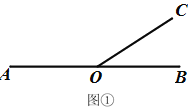
【题目】已知：如图1，点O是直线AB上一点，过点O作射线OC.

(1)若∠AOC=140°，则∠BOC=________°.

(2)在图1中分别画∠AOC的角平分线OE和∠BOC的角平分线OF，那么,OE和OF有什么位置关系，请说明理由.

(3)若∠BOC=30°，射线OD从OB出发，绕点O以每秒10°角的速度逆时针旋转.当射线OD与射线OA重合时，射线OC以每秒30°角的速度绕点O逆时针旋转，射线OD按原来的速度和方向继续旋转，当射线OC或射线OD中有一条射线与射线OB重合时，两条射线都停止.设射线OD旋转的时间为t秒，在旋转的过程中，是否存在某个时刻，使得射线OB、OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在，直接写出所有满足条件的t的值，若不存在，说明理由.