
【题目】观察下列各式:
13=![]() ×12×22
×12×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
13+23+33+43=100=![]() ×42×52
×42×52
回答下面的问题:
(1)猜想:13+23+33+…+(n-1)3+ n3=________.
(2)利用你得到的(1)中的结论,计算13+23+33+…+993+1003的值.
(3)计算:213+223+…+993+1003的值.
【答案】(1)![]() n2(n+1)2(2) 25502500;(3) 25458400.
n2(n+1)2(2) 25502500;(3) 25458400.
【解析】
(1)(2)观察已知的等式,发现:等式的左边是连续自然数的立方和,等式的右边是连续自然数的和的平方;由此得出答案即可;
(3)根据(1)中发现的结论,即可求得结论.
(1)∵13=![]() ×12×22
×12×22
13+23=9=![]() ×22×32
×22×32
13+23+33=36=![]() ×32×42
×32×42
13+23+33+43=100=![]() ×42×52
×42×52
…
∴猜想:13+23+33+…+(n-1)3+ n3=![]() n2(n+1)2;
n2(n+1)2;
故填:![]() n2(n+1)2
n2(n+1)2
(2) 13+23+33+…+993+1003=![]() ×1002×1012=25502500;
×1002×1012=25502500;
(3) 213+223+…+993+1003
=13+23+33+…+993+1003(13+23+33+43+…203)
= ![]() ×1002×1012
×1002×1012![]() ×202×212
×202×212
=25458400.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】某校为了迎接体育中考,了解学生的体质情况,学校随机调查了本校九年级![]() 名学生“
名学生“![]() 秒跳绳”的次数,并将调查所得的数据整理如下:
秒跳绳”的次数,并将调查所得的数据整理如下:
![]() 秒跳绳次数的频数、频率分布表
秒跳绳次数的频数、频率分布表
![]() 秒跳绳次数的频数分布直方图
秒跳绳次数的频数分布直方图
 、
、
根据以上信息,解答下列问题:
(1)表中,![]() ,
,![]() ;
;
(2)请把频数分布直方图补充完整;
(3)若该校九年级共有![]() 名学生,请你估计“
名学生,请你估计“![]() 秒跳绳”的次数
秒跳绳”的次数![]() 以上(含
以上(含![]() 次)的学生有多少人?
次)的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为E,如果AB=5,AE=4,BC=8,有下列结论:
①DE=4![]() ;
;
②S△AED=![]() S四边形ABCD;
S四边形ABCD;
③DE平分∠ADC;
④∠AED=∠ADC.
其中正确结论的序号是_____(把所有正确结论的序号都填在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
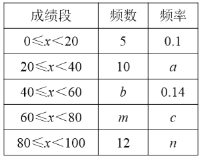
【题目】某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳绳 | 25 | a |
实心球 | 20 |
|
50m | b | 0.4 |
拔河 | 0.15 |
(1)直接写出a= ,b= ;
(2)将图中的扇形统计图补充完整(注明项目、百分比);
(3)若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2012年7月1日起某市执行新版居民阶梯电价,小明同学家收到了新政后的第一张电费单,小明爸爸说:“小明,请你计算一下,这个月的电费支出与新政前相比是多了还是少了?”于是小明上网了解了有关电费的收费情况,得到如下两表:
2004年1月至2012年6月执行的收费标准:
月用电量(度)50度有以下部分 | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
单价(元/度) | 0.53 | 0.56 | 0.63 |
2012年7月起执行的收费标准:
月用电量(度) | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
单价(元/度) | 0.53 | 0.58 | 0.83 |
(1)若小明家2012年7月份的用电量为200度,则小明家7月份的电费支出是多少元?比新政前少了多少元?
(2)若新政后小明家的月用电量为a度,请你用含a的代数式表示当月的电费支出.
查看答案和解析>>
科目:初中数学 来源: 题型:
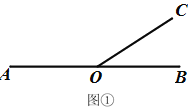
【题目】已知:如图1,点O是直线AB上一点,过点O作射线OC.
(1)若∠AOC=140°,则∠BOC=________°.
(2)在图1中分别画∠AOC的角平分线OE和∠BOC的角平分线OF,那么,OE和OF有什么位置关系,请说明理由.
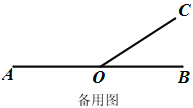
(3)若∠BOC=30°,射线OD从OB出发,绕点O以每秒10°角的速度逆时针旋转.当射线OD与射线OA重合时,射线OC以每秒30°角的速度绕点O逆时针旋转,射线OD按原来的速度和方向继续旋转,当射线OC或射线OD中有一条射线与射线OB重合时,两条射线都停止.设射线OD旋转的时间为t秒,在旋转的过程中,是否存在某个时刻,使得射线OB、OC与OD中的某一条射线是另两条射线所夹角的平分线?若存在,直接写出所有满足条件的t的值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,直线l切⊙O于A,在直线l上取点B,AB=4.
(1)请用无刻度的直尺和圆规,过点B作直线m⊥l,交⊙O于C、D(点D在点C的上方);(保留作图痕迹,不要求写作法)
(2)求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com