练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中Rt△ABC的斜边BC在x轴上，点B坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后再向下平移2个单位，则A点的对应点A′的坐标为（　　）

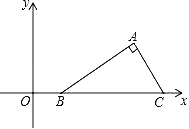
    A. （﹣4，﹣2﹣） B. （﹣4，﹣2+） C. （﹣2，﹣2+） D. （﹣2，﹣2﹣）

    【答案】D

    【解析】解：作AD⊥BC，并作出把Rt△ABC先绕B点顺时针旋转180°后所得△A1BC1，如图所示．∵AC=2，∠ABC=30°，∴BC=4，∴AB=2，∴AD===，∴BD===3．∵点B坐标为（1，0），∴A点的坐标为（4，）．∵BD=3，∴BD1=3，∴D1坐标为（﹣2，0），∴A1坐标为（﹣2，﹣）．∵再向下平移2个单位，∴A′的坐标为（﹣2，﹣﹣2）．故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列方程没有实数根的是（　　）

    A. x3+2＝0B. x2+2x+2＝0

    C. ＝x﹣1D. ＝0

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：若以一条线段为对角线作正方形，则称该正方形为这条线段的“对角线正方形”．例如，图①中正方形ABCD即为线段BD的“对角线正方形”．如图②，在△ABC中，∠ABC=90°，AB=3cm，BC=4cm，点P从点C出发，沿折线CA﹣AB以5cm/s的速度运动，当点P与点B不重合时，作线段PB的“对角线正方形”，设点P的运动时间为t（s），线段PB的“对角线正方形”的面积为S（cm2）．

    （1）如图③，借助虚线的小正方形网格，画出线段AB的“对角线正方形”．

    （2）当线段PB的“对角线正方形”有两边同时落在△ABC的边上时，求t的值．

    （3）当点P沿折线CA﹣AB运动时，求S与t之间的函数关系式．

    （4）在整个运动过程中，当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学七年级A班有50人,某次活动中分为三组,第一组有(3a+4b+2)人,第二组比第一组的一半多6人.

    (1)求第三组的人数;(用含a,b的整式表示)

    (2)试判断当a=1,b=2时,是否满足题意.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小明设计的“作平行四边形ABCD的边AB的中点”的尺规作图过程．

    已知：平行四边形ABCD．

    求作：点M，使点M 为边AB 的中点．

    作法：如图，

    ①作射线DA；

    ②以点A 为圆心，BC长为半径画弧，

    交DA的延长线于点E；

    ③连接EC 交AB于点M ．

    所以点M 就是所求作的点．

    根据小明设计的尺规作图过程，

    (1)使用直尺和圆规，补全图形 (保留作图痕迹)；

    (2)完成下面的证明．

    证明：连接AC，EB．

    ∵四边形ABCD 是平行四边形，

    ∴AE∥BC．

    ∵AE= ，

    ∴四边形EBCA 是平行四边形( )(填推理的依据) ．

    ∴AM =MB ( )(填推理的依据) ．

    ∴点M 为所求作的边AB的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

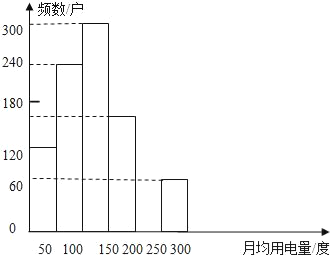
    【题目】近期，中宣部、国家发改委发出开展节俭养德全民节约行动的通知，在全社会营造厉行节约、拒绝浪费的浓厚氛围，我市某中学为了解该校学生家庭月均用电量情况，给学生布置了收集自己家中月均用电量数据的课外作业，学校随机抽取了1000名学生家庭月均用电量的数据，并将调查数据整理如下：

    月均用电量a/度

    频数/户

    频率

    0≤a＜50

    120

    0.12

    50≤a＜100

    240

    n

    100≤a＜150

    300

    0.30

    150≤a＜200

    m

    0.16

    200≤a＜250

    120

    0.12

    250≤a＜300

    60

    0.06

    合　　计

    1000

    1

    （1）频数分布表中的m=_____，n=_____；

    （2）补全频数分布直方图；

    （3）被调查的1000名学生家庭月均用电量的众数落在哪一个范围？

    （4）求月均用电量小于150度的家庭数占被调查家庭总数的百分比．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在中，AB=AC，∠ABC =，D是BC边上一点，以AD为边作，使AE=AD，+=180°．

    （1）直接写出∠ADE的度数（用含的式子表示）；

    （2）以AB，AE为边作平行四边形ABFE，

    ①如图2，若点F恰好落在DE上，求证：BD=CD；

    ②如图3，若点F恰好落在BC上，求证：BD=CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】体育课上，甲、乙两个小组进行定点投篮对抗赛，每组10人，每人投10次．下表是甲组成绩统计表：

    投进个数

    10个

    8个

    6个

    4个

    人数

    1个

    5人

    2人

    2人

    (1)请计算甲组平均每人投进个数；

    (2)经统计，两组平均每人投进个数相同且乙组成的方差为3.2．若从成绩稳定性角度看，哪一组表现更好？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣x2+bx+c与x轴分别交于点A、B，与y轴交于点C，且OA=1，OB=3，顶点为D，对称轴交x轴于点Q．

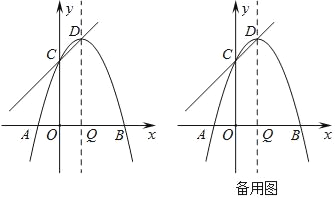
    （1）求抛物线对应的二次函数的表达式；

    （2）点P是抛物线的对称轴上一点，以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P的坐标；

    （3）在抛物线的对称轴上是否存在一点M，使得△DCM∽△BQC？如果存在，求出点M的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案