练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

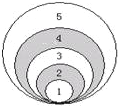
    【题目】如图：同学们在操场的一个圆形区域内玩投掷沙包的游戏，圆形区域由5个过同一点且半径不同的圆组成．经过多次实验，发现沙包如果都能落在区域内时，落在2、4两个阴影内的概率分别是0.36和0.21，设最大的圆的直径是5米，则1、3、5三个区域的面积和是_____．

    【答案】2.6875πm2．

    【解析】

    根据题意，可得大圆的面积，再由几何概率的意义，可得第2、4两个阴影的面积所占的比例，进而可得1、3、5三个区域的面积和占的比例，计算可得其面积之和．

    根据题意得，最大的圆的直径是5米，则大圆的面积为6.25πm2，
    又有落在2、4两个阴影内的概率分别是0.36和0.21，
    则第2、4部分的面积和占总面积的0.36+0.21=0.57，即57%，
    则1、3、5三个区域的面积占总面积的1-0.57=0.43，即43%，
    故1、3、5三个区域的面积和为6.25π×0.43=2.6875π m2．
    故答案是：2.6875π m2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

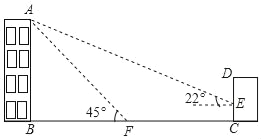
    【题目】如图，小明想测量学校教学楼的高度，教学楼AB的后面有一建筑物CD，他测得当光线与地面成22°的夹角时，教学楼在建筑物的墙上留下高2米高的影子CE；而当光线与地面成45°的夹角时，教学楼顶A在地面上的影子F与墙角C有13米的距离（点B，F，C在同一条直线上），则AE之间的长为_____米．（结果精确到lm，参考数据：sin22°≈0.375，cos22°≈0.9375，tan22°≈0.4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线形拱桥，当拱顶离水面2m时，水面宽4m，则水面下降1m时，水面宽度增加_____m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

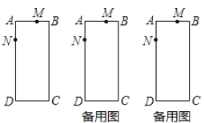
    【题目】长方形中，，点和点都是从点出发，点在这个长方形的边上顺时针运动，点在这个长方形的边上逆时针运动，它们的速度都是每秒1个单位，设它们的运动时间是秒

    （1）时，求线段的长；

    （2）在运动过程中，连接，设线段和点所经过的路线所组成的封闭的图形面积是，求出与的函数关系式，并注明的取值范围．

    （3）在上一问中，是否存在某个时刻，使得是长方形面积的一半？若存在，求出；若不存在，请说明理由．

    （4）当点在上运动时（不包括点），存不存在某一时刻，使得是直角三角形吗？若存在，求出；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．

    （1）求抛物线的解析式；

    （2）当点P运动到什么位置时，△PAB的面积有最大值？

    （3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于的一元二次方程.

    （1）试证明：无论取何值此方程总有两个实数根；

    （2）若原方程的两根，满足，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】作图题:

    （1）过点A画高AD；

    （2）过点B画中线BE；

    （3）过点C画角平分线CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点在线段上，现将沿着翻折后得到，交于点，且，若，则的面积为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M、N．AH⊥MN于点H．

    （1）当∠MAN绕点A旋转到BM=DN时，请你直接写出线段AH与AB的数量关系______．（不需证明）

    （2）当∠MAN绕点A旋转到BM≠DN时，问（1）中线段AH与AB的数量关系还成立吗？若成立，给出证明，若不成立，说明理由．

    查看答案和解析>>

    同步练习册答案