
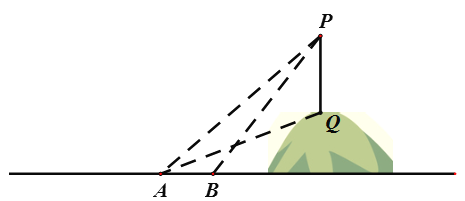
【题目】为了测量山坡上的电线杆PQ的高度,某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下,他们在A处测得信号塔顶端P的仰角是45°,信号塔底端点Q的仰角为30°,沿水平地面向前走100米到B处,测得信号塔顶端P的仰角是60°,求信号塔PQ得高度。
科目:初中数学 来源: 题型:
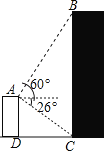
【题目】如图所示,小明在自家楼顶上的点A处测量建在与小明家楼房同一水平线上邻居的电梯楼的高度,测得电梯楼顶部B处的仰角为60°,底部C处的俯角为26°,已知小明家楼房的高度AD=15米,求电梯楼的高度BC.(结果精确到0.1米,参考数据:![]() ≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
≈1.73,sin26°≈0.44,cos26°≈0.90,tan26°≈0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() ,
,![]() ;
;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
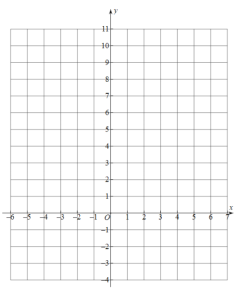
(3)观察函数图象:
①当方程![]() 有且仅有两个不相等的实数根,根据函数图象直接写出
有且仅有两个不相等的实数根,根据函数图象直接写出![]() 的取值范围为 ;
的取值范围为 ;
②在该平面直角坐标系中画出直线![]() 的图象,根据图象直接写出该直线与函数
的图象,根据图象直接写出该直线与函数![]()
![]() 的交点横坐标为: (结果保留一位小数).
的交点横坐标为: (结果保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)某种电子产品共![]() 件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为
件,其中有正品和次品.已知从中任意取出一件,取得的产品为次品的概率为![]() .
.
(1)该批产品有正品 件;
(2)如果从中任意取出![]() 件,利用列表或树状图求取出
件,利用列表或树状图求取出![]() 件都是正品的概率.
件都是正品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
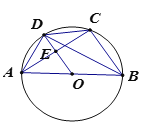
【题目】如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙D于点D,交AC于点E,连接AD,BD,CD若AB=10,cos∠ABC=![]() ,则tan∠DBC的值是( )
,则tan∠DBC的值是( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
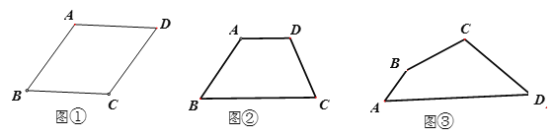
如图①菱形ABCD中,AB=4,∠ABC=60°点0是菱形ABCD两条对角线的交点,EF是经过点O的任意一条线段,容易知道线段EF将菱形ABCD的面积等分,那么线段EF的长度的最大值是 ,最小值是 。
问题探究:
如图② 四边形ABCD中,AD∥BC,AD=2,BC=4,∠B=∠C=60°,请你过点D画出将四边形ABCD面积平分的线段DE,并求出DE的长。
问题解决:
如图③.四边形ABCD是西安城区改造过程中一块不规则空地,为了美化环境,市规划办决定在这块地里种两种花弃,打算过点C修一条笔直的通道,以方便市民出行和观赏花卉,并要求通道两侧种植的花卉面积相等,经测量AB=20米,AD=100米,∠A=60°,∠ABC=150°,∠BCD=120°,若将通道记为CF,请你画出通道CF,并求出通道CF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过抛物线y=ax2+bx上一点A(4,﹣2)作x轴的平行线,交抛物线于另一点B,点C在直线AB上,抛物线交x轴正半轴于点D(2,0),点B与点E关于直线CD对称.
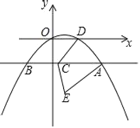
(1)求抛物线的表达式;
(2)①若点E落在抛物线的对称轴上,且在x轴下方时,求点C的坐标.②AE最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
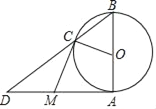
【题目】如图,AB是⊙O的直径,且AB=6,点M为⊙O外一点,且MA,MC分别切⊙O于点A、C.点D是两条线段BC与AM延长线的交点.
(1)求证:DM=AM;
(2)直接回答:
①当CM为何值时,四边形AOCM是正方形?
②当CM为何值时,△CDM为等边三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则:①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣l<x<3,其中正确的是( )
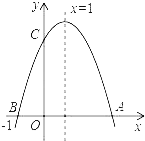
A.①②④B.②④C.①④D.②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com