
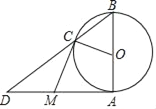
【题目】如图,AB是⊙O的直径,且AB=6,点M为⊙O外一点,且MA,MC分别切⊙O于点A、C.点D是两条线段BC与AM延长线的交点.
(1)求证:DM=AM;
(2)直接回答:
①当CM为何值时,四边形AOCM是正方形?
②当CM为何值时,△CDM为等边三角形?
【答案】(1)见解析;(2)①当CM=OA=3时,四边形AOCM是正方形;②![]() .
.
【解析】
(1)根据切线的性质得:MA⊥OA,MC⊥OC,证明△MAO≌△MAO(HL),得MC=MA,根据等边对等角得:∠2=∠B,由等角的余角相等可得结论;
(2)①直接可得CM=OA=3;
②先根据等边三角形定义可得:DM=CM,∠D=60°,证明Rt△OCM≌△OAM(HL),得CM=AM=DM,可得结论.
(1)连接OM,如图1,
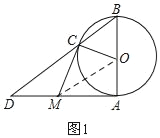
∵MA,MC分别切⊙O于点A、C,
∴MA⊥OA,MC⊥OC,
在Rt△MAO和Rt△MCO中,
MO=MO,AO=CO,
∴△MAO≌△MAO(HL),
∴MC=MA,
∵OC=OB,
∴∠OCB=∠B,
又∵∠DCM+∠OCB=90°,∠D+∠B=90°,
∴∠DCM=∠D,
∴DM=MC,
∴DM=MA;
(2)如图2,
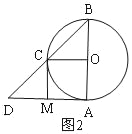
①当CM=OA=3时,四边形AOCM是正方形;
②连接OM,如图3,

∵△DCM是等边三角形,
∴CM=DM,∠D=60°,
∵∠DAB=90°,
∴∠B=30°,
∴∠AOC=2∠B=60°,
∵AB=6,
∴tan∠B=tan30°=![]() =
=![]() ,
,
∴AD=2![]() ,
,
设CM=x,
∵OC=OA,OM=OM,
∴Rt△OCM≌△OAM(HL),
∴CM=AM=DM,
∴CM=![]() AD=
AD=![]()


科目:初中数学 来源: 题型:
【题目】已知顶点为(-3,-6)的抛物线![]() 经过点(-1,-4),下列结论中错误的是( )
经过点(-1,-4),下列结论中错误的是( )

A. ![]()
B. 若点(-2, ![]() ),(-5,
),(-5, ![]() ) 在抛物线上,则
) 在抛物线上,则![]()
C. ![]()
D. 关于![]() 的一元二次方程
的一元二次方程![]() 的两根为-5和-1
的两根为-5和-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织“优质课大赛”活动,经过评比有两名男教师和两名女教师获得一等奖,学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛,挑选的两位教师恰好是一男一女的概率为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
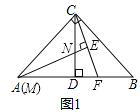
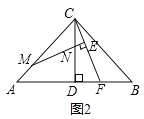
【题目】如图:已知△ABC中,CA=CB,CD⊥AB于D点,点M为线段AC上一动点,线段MN交DC于点N,且∠BAC=2∠CMN,过点C作CE⊥MN交MN延长线于点E,交线段AB于点F,探索![]() 的值.
的值.
(1)若∠ACB=90°,点M与点A重合(如图1)时:①线段CE与EF之间的数量关系是 ;②![]() = ;
= ;
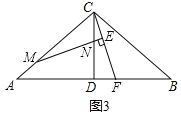
(2)在(1)的条件下,若点M不与点A重合(如图2),请猜想写出![]() 的值,并证明你的猜想
的值,并证明你的猜想
(3)若∠ACB≠90°,∠CAB=![]() ,其他条件不变,请直接写出
,其他条件不变,请直接写出![]() 的值(用含有
的值(用含有![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡在推进村村通公路某项目建设中,计划修建公路15千米.已知甲队单独完成修建公路所需得时间是乙队得1.5倍,甲队每天比乙队少修0.5千米.
(1)求甲、乙两队单独完成修建公路各需多少天?
(2)已知甲队每天的工作费用是4000元,乙队每天的工作费用是5000元,若该工程由甲乙两队合作完成,且工程的总费用不超过52000元,求乙队至少要工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.
(1)若![]() ,函数图象与
,函数图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() 的值;
的值;
(2)若![]() ,
,![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,求证:
,求证:![]() ;
;
(3)若![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 在
在![]() 时,
时,![]() 随
随![]() 的增大而增大?若存在,求
的增大而增大?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地高速铁路建设成功.试运行期间,一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发.设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示y与x之间的函数关系,根据图象分析出以下信息:①甲乙两地相距1000千米;②动车从甲地到乙地共需要4个小时;③![]() 表示的实际意义是动车的速度;④普通列车的速度是
表示的实际意义是动车的速度;④普通列车的速度是![]() 千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
千米/小时;⑤动车到达乙地停留2小时后返回甲地,在普通列车出发后7.5小时和动车再次相遇.以上信息正确的是( )
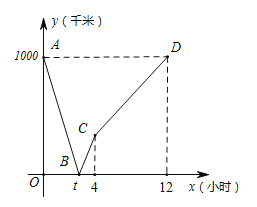
A.①②④B.①③④⑤C.①②④⑤D.②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com