
���� ��1�����ݶ�����ڽǺͶ��������CDP+��CEP�Ķ����������ڲ��������1+��2=360��-����CDP+��CEP��������������ɣ�
��2�����ݶ�����ڽǺͶ��������CDP+��CEP�Ķ����������ڲ��������1+��2=360��-����CDP+��CEP��������������ɣ�
��3������������������������COD=��2+�Ϧ��������������ڽǺͶ��������C+��COD+��CDO=180�㣬�����ڲ��ǵó���CDO=��180��-��1���Ƴ���2+�Ϧ�+180��-��1+90��=180�㼴�ɣ�
��4�������ڲ��ǵó���CDP=180��-��1����CEO=180��-��2�������������ڽǺͶ����ó���POD+�Ϧ�+��PDO=��C+��CEO+��COE=180�㣬����Ϧ�+180��-��1=90��+180��-��2�����ɵó��𰸣�
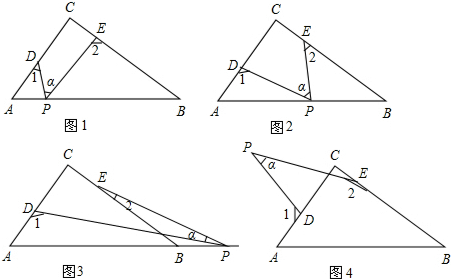
��� �⣺��1����ͼ1��
�ߡ�CDP+��CEP=360��-��DPE-��C=360��-50��-90��=220�㣬
���1+��2=180��-��CDP+180��-��CEP
=360��-����CDP+��CEP��
=140�㣻
��2��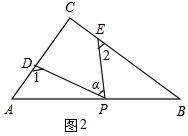
��ͼ2����1+��2=90��+�Ϧ���
�����ǣ��ߡ�CDP+��CEP=360��-��DPE-��C=360��-�Ϧ�-90��=270��-�Ϧ���
���1+��2=180��-��CDP+180��-��CEP
=360��-����CDP+��CEP��
=360��-��270��-�Ϧ���
=90��+�Ϧ���
�ʴ�Ϊ��90��+�Ϧ���
��3����1=90��+��2+�Ϧ���
�����ǣ���ͼ3��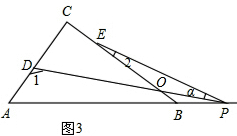
�ߡ�COD=��2+�Ϧ�����C+��COD+��CDO=180�㣬��CDO=��180��-��1����C=90�㣬
���2+�Ϧ�+180��-��1+90��=180�㣬
���1=90��+��2+�Ϧ���
�ʴ�Ϊ����1=90��+��2+�Ϧ���
��4����2=90��+��1-�Ϧ���
�����ǣ���ͼ4��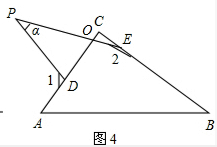
�ߡ�CDP=180��-��1����POD+�Ϧ�+��PDO=��C+��CEO+��COE=180�㣬��COE=��POD����C=90�㣬��CEO=180��-��2��
��Ϧ�+180��-��1=90��+180��-��2��
���2=90��+��1-�Ϧ���ͼ
�ʴ�Ϊ����2=90��+��1-�Ϧ���
���� ���⿼�����ڲ��Ƕ��壬������������ʣ��������ڽǺͶ�����Ӧ�ã����ۺ����ö������������ǽ����Ĺؼ�����Ŀ�Ƚϵ��ͣ��Ѷ����У�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
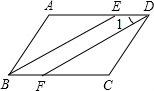 ��ͼ���ı���ABCD��ƽ���ı��Σ���ABC=78�㣬BEƽ�֡�ABC�ҽ�AD�ڵ�E��DF��BE�ҽ�BC�ڵ�F�����1�Ķ���Ϊ39�㣮
��ͼ���ı���ABCD��ƽ���ı��Σ���ABC=78�㣬BEƽ�֡�ABC�ҽ�AD�ڵ�E��DF��BE�ҽ�BC�ڵ�F�����1�Ķ���Ϊ39�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
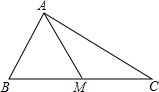 ��ͼ��AM�ǡ�ABC�����ߣ�����ABM�����Ϊ4�����ABC�����Ϊ��������
��ͼ��AM�ǡ�ABC�����ߣ�����ABM�����Ϊ4�����ABC�����Ϊ��������| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
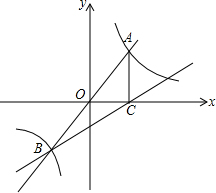 ��֪����������y=$\frac{k}{x}$��ֱ��y=x-1��ֱ��y=2x�����ཻ��B������������y=2x��y=$\frac{k}{x}$�ཻ��A��y=x-1��x����C����S��ABC���ڣ�������
��֪����������y=$\frac{k}{x}$��ֱ��y=x-1��ֱ��y=2x�����ཻ��B������������y=2x��y=$\frac{k}{x}$�ཻ��A��y=x-1��x����C����S��ABC���ڣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com